Середня кількість зіткнень молекул. Середня довжина вільного пробігу

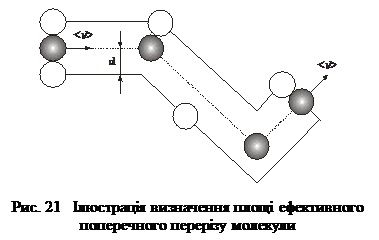Хаотичний рух молекул газу супроводжується їхніми зіткненнями. Протягом проміжку часу Dt між двома послідовними зіткненнями молекула проходить певний відрізок шляху l, який називають довжиною вільного пробігу. Очевидно, що за великої кількості зіткнень, яких зазнає молекула, зна-чення l є різним, тому вводять поняття <l> середньої довжи-ни вільного пробігу.

Під час зіткнень від-стань між молекулами стає мінімальною. Цю відстань називають ефективним газокінетичним діаметром молекули d (рис. 2.6). Величина s=pd² – це ефективний поперечний переріз молекули. Зіткнення – це ймовірнісний процес. Обчислимо ймовірність зіткнення молекули з іншою з таких міркувань.

Нехай молекула А рухається вздовж Ох і потрапляє в об’єм dV=Sdx, у якому містяться інші молекули (умовно їх уважатимемо нерухомими).

Кількість молекул у цьому об’ємі

dN=n₀Sdx. (2.37 )

Сумарна площа перерізу цих молекул

dS=sdN=s n₀Sdx. (2.38)

Тоді ймовірність зіткнень молекули А з молекулою в об’ємі dV

dw= 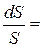s n₀dx, (2.39)

у цьому разі w=s n₀x. За умови x >> <l> імовірність зіткнення дорівнює одиниці, отже,s n₀<l>=1, звідки

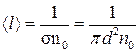. (2.40)

Як бачимо, середня довжина вільного пробігу – це шлях, на якому ймовірність зіткнення дорівнює одиниці.

Обчислимо тепер середню кількість зіткнень молекули за одиницю часу. Очевидно, що за час Dt молекула проходить шлях

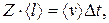(2.41)

де 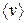– середня швидкість поступального руху молекули; Z – кількість зіткнень. Тоді за 1 с молекула зазнає 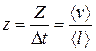зіткнень або, на підставі (2.41),

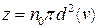. (2.42)

Досі ми вважали, що рухається лише одна молекула, а інші – нерухомі. З урахуванням руху інших молекул отримаємо

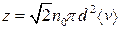(2.43 )

За допомогою рівняння стану газу р=nkT можна довести, що

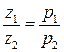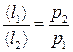або . (2.44)

Отже, з підвищенням тиску кількість зіткнень зростає, а довжина вільного пробігу зменшується.