Взаимодействие молекул. Средняя длина свободного пробега

Столкновением молекул будем называть процесс их взаимодействия, в результате которого изменяются скорости молекул.

Характер взаимодействия молекул можно представить, если рассмотреть зависимость потенциальной энергии взаимодействия молекул от расстояния между их центрами. Эта зависимость имеет вид, приближенно показанный на рисунке 11.2.

Представим, что одна молекула находится в начале координат, а вторая приближается к ней из «бесконечности», имея очень небольшую кинетическую энергию. На расстояниях, превышающих 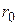_, взаимодействие молекул имеет характер притяжения. Действительно, для с увеличением расстояния между молекулами потенциальная энергия возрастает. Это означает, что ее градиент направлен в сторону увеличения расстояния между молекулами, а сила взаимодействия ( 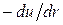) направлена в сторону уменьшения расстояния между молекулами. Поэтому при сближении молекул их взаимная скорость возрастает: потенциальная энергия взаимодействия преобразуется в кинетическую, приближающаяся молекула разгоняется.

На расстояниях менее 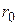притяжение сменяется быстро возрастающим отталкиванием. Потенциальная энергия взаимодействия резко возрастает (кинетическая преобразуется в потенциальную), и при ее равенстве начальной кинетической энергии молекулы останавливаются. Далее происходят обратные процессы, молекулы разлетаются.

Минимальное расстояние d, на которое сближаются при соударении центры молекул, называется эффективным диаметром молекулы. Величина 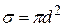называется эффективнымсечениеммолекулы. 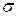равно площади поперечного сечения цилиндра, по оси которого движется данная молекула, такого, что если центр другой молекулы попадает в объем цилиндра, то молекулы должны столкнуться.

Понятно, что при увеличении температуры центры молекул при соударениях будут сближаться сильнее, поэтому эффективный диаметр зависит от температуры. Следует иметь в виду, что рост потенциальной энергии отталкивания происходит очень быстро, поэтому зависимость эффективного диаметра от температуры имеет место обязательно, но выражена не очень сильно.

За секунду молекула проходит в среднем путь, равный ее средней скорости 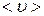. Если за секунду она претерпевает 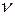столкновений, тосредняядлинасвободногопробега молекулы

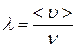(11.9).

Для расчета 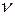предположим, что все молекулы, кроме данной, покоятся на своих местах. Ударившись об одну из неподвижных молекул, данная будет лететь прямолинейно до соударения с другой. Очередное столкновение произойдет в том случае, если центр неподвижной молекулы окажется от прямой, вдоль которой летит данная молекула, на расстоянии меньшим эффективного диаметра. За секунду молекула столкнется со всеми молекулами, центры которых попадают в объем коленчатого цилиндра с основанием 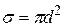и длинной, равной средней скорости 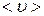. Если концентрация молекул равна n, то число соударений на этом пути

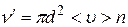(11.9)

Необходимо учесть, что на самом деле движутся все молекулы, и в (11.9) необходимо учитывать не 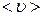, а среднюю относительную скорость движения молекул, которая в 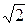раз больше. Тогда для средней длины свободного пробега l можем записать:

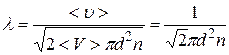(11.10)

Представляет интерес количественная оценка l и 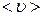. Будем считать, что в жидкости молекулы находятся на небольших расстояниях друг от друга. Тогда корень третьей степени из объема, приходящегося на одну молекулу, даст нам оценку размеров молекулы. Один моль воды занимает объем 18*10^{-10 м3} и содержит число Авогадро 6*10²³ молекул. Тогда на одну молекулу приходится » 30*10^{-30 м3}, а диаметр молекулы » 3*10^{-10 м. При условиях, близких к нормальным, один моль газа занимает объем 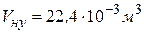. Тогда концентрацию молекул при нормальных условиях можно оценить по формуле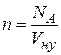} , а среднюю длину свободного пробега в соответствии с формулой (11.10)

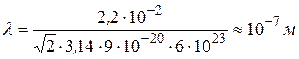
Отметим, что 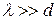, а это означает, что при вычислениях объема коленчатого цилиндра мы справедливо пренебрегли тем, что основания не перпендикулярны оси.

Средняя скорость при нормальных условиях составляет порядка 5*10² м/с. Разделив эту величину на l на, получим оценку количества соударений молекулы в единицу времени: 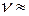=5*10⁹ c^-1.