Вектор скорости. Средняя и мгновенная скорость.
 Движения различных тел различаются тем, что тела за одинаковые промежутки (равные) времени проходят различные по величине пути. Для характеристики такого движения вводят понятие скорости.
Движения различных тел различаются тем, что тела за одинаковые промежутки (равные) времени проходят различные по величине пути. Для характеристики такого движения вводят понятие скорости.
1) Введем понятие среднейскорости ( 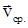 ) – это величина, равная отношению перемещения
) – это величина, равная отношению перемещения 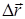 к тому промежутку времени, в течение которого это перемещение произошло
к тому промежутку времени, в течение которого это перемещение произошло 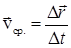 .
.
2) За малый промежуток времени Dt точка проходит путь DS, совершая перемещение 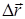 (рис. 2.6). При Dt®0 отношения
(рис. 2.6). При Dt®0 отношения 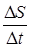 и
и 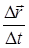 практически перестают изменяться как по величине, так и по направлению и стремятся к определенному пределу
практически перестают изменяться как по величине, так и по направлению и стремятся к определенному пределу
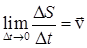 и
и 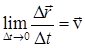
который будет выражать вектор мгновеннойскорости, т.е. скорости в данный момент времени.
В математике данный предел называется производной, следовательно, скорость можно определить как производную радиус-вектора движущейся точки по времени:
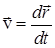 или по модулю
или по модулю 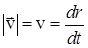 .
.
При бесконечном уменьшении Dt различие между DS и 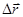 будет уменьшаться и в пределе они совпадут, тогда можно записать, что модуль скорости
будет уменьшаться и в пределе они совпадут, тогда можно записать, что модуль скорости
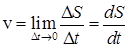 , (2.1)
, (2.1)
т.е. мгновенная скорость при неравномерном движении численно равна первой производной пути по времени.
Итак, вектор мгновенной скорости в любой точке траектории направлен по касательной к траектории (и совпадает с направлением вектора перемещения) и численно равен первой производной пути по времени.
Единица измерения v: [v]=м/с.
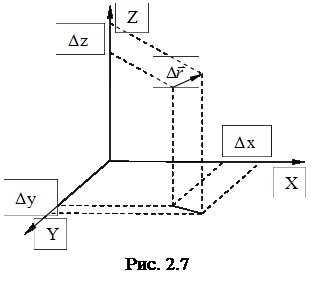
Если рассматривать движение в пространстве, то величину и направление вектора скорости можно представить через проекции этого вектора на направления осей x, y, z (рис. 2.7).
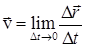 ;
;
где 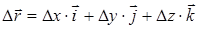 ,
,
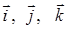 – единичные вектора по осям x, y, z.
– единичные вектора по осям x, y, z.
Тогда
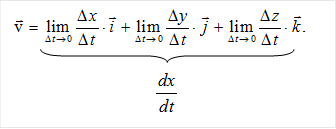
Следовательно, 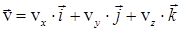
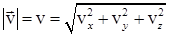
Дата добавления: 2015-11-04; просмотров: 1507;
