ЦИКЛ КАРНО.
Для работы теплового двигателя необходимо наличие двух тепловых резервуаров. Один из них с температурой более высокой будем называть нагревателем. Его температура Т1. Другой, с более низкой температурой Т2, будет называться холодильником. Будем считать, что теплоемкости резервуаров бесконечны, т. е. отнятие или сообщение им конечного тепла не изменяет их температуру.
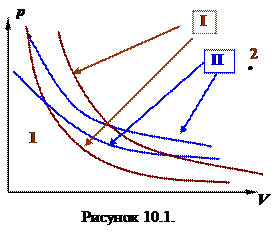 Протекающий в рабочем теле процесс, сопровождающийся теплообменом с резервуарами, может быть обратимым только в том случае, если температура тела будет равна температуре резервуара. Действительно, если тело получает тепло, находясь при температуре ниже, чем ТI, то при обратном ходе процесса тело сможет отдать тепло, находясь при температуре не ниже, чем ТI. Но тогда прямой и обратный ход процесса не будет совпадать и он не будет обратимым. Таким образом, обмен теплом с резервуаром и может быть только обратимыми изотерми-ческим, причем температура тела и резервуара должна быть одинаковой.
Протекающий в рабочем теле процесс, сопровождающийся теплообменом с резервуарами, может быть обратимым только в том случае, если температура тела будет равна температуре резервуара. Действительно, если тело получает тепло, находясь при температуре ниже, чем ТI, то при обратном ходе процесса тело сможет отдать тепло, находясь при температуре не ниже, чем ТI. Но тогда прямой и обратный ход процесса не будет совпадать и он не будет обратимым. Таким образом, обмен теплом с резервуаром и может быть только обратимыми изотерми-ческим, причем температура тела и резервуара должна быть одинаковой.
Другим обратимым процессом, который может совершать рабочее тело при совершении обратимого цикла в рассматриваемых условиях является адиабатический процесс. Таким образом, обмениваясь теплом с двумя тепловыми резервуарами, тело может совершать цикл, состоящий из двух изотерм и двух адиабат. Такой цикл называется цикломКарно.
При обратимом адиабатическом процессе dQ = 0, а значит dS = 0. Следовательно, такой процесс можно назвать изоэнтропическим. Таким образом на диаграмме Т, S цикл Карно будет представлять из себя прямоугольник. Площадь под некоторой кривой на диаграмме Т, S выражается интегралом 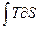 , который равен количеству тепла, получаемого системой в ходе рассматриваемого процесса. Следовательно, площадь цикла на диаграмме T, S дает количество тепла, полученного системой за цикл, аналогично тому, как на диаграмме P, V площадь цикла равна работе, совершаемой системой за цикл.
, который равен количеству тепла, получаемого системой в ходе рассматриваемого процесса. Следовательно, площадь цикла на диаграмме T, S дает количество тепла, полученного системой за цикл, аналогично тому, как на диаграмме P, V площадь цикла равна работе, совершаемой системой за цикл.
Найдем к. п. д. Цикла Карно. Поскольку в ходе цикла рабочее вещество (тело, система) возвращается в исходное состояние, то полное изменение энтропии за цикл равно нулю: 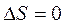 .
.
Энтропия тела изменяется только в ходе изометрических процессов. В ходе изотермического процесса 1-2 изменение энтропии.
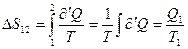 (12)
(12)
На участке 4 тело отдает резервуару количество тепла Q¢2 , что эквивалентно получению тепла – Q¢2. Следовательно, изменение энтропии.
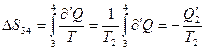 (13)
(13)
Учитывая что, 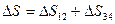 получаем, что
получаем, что
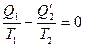 откуда
откуда 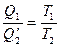 (14)
(14)
С учетом (14), для к. п. д. Получаем выражение:
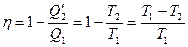 (15)
(15)
При выводе соотношения (15) мы не делали никаких предложений о свойствах рабочего тела и устройстве тепловой машины. Следовательно, можно сформулировать теорему Карно: к. п. д. всех обратимых машин, работающих с данным нагревателем и холодильником одинаковы и определяются только температурами нагревателя и холодильника.
Можно доказать, что кпд необратимой машины, работающей с теми же нагревателем и холодильником, будет меньше, чем у обратимой. На каждом участке необратимого цикла 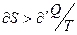 Следовательно,
Следовательно,
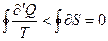 (16)
(16)
Интеграл 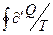 можно разбить на четыре слагаемых:
можно разбить на четыре слагаемых:
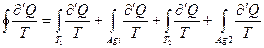 (17)
(17)
На адиабатических участках 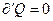 , и соответствующие интегралу, также равны нулю. При необратимом процессе в знаменателе отношения
, и соответствующие интегралу, также равны нулю. При необратимом процессе в знаменателе отношения 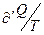 состоит температура резервуара, от которого тело получает тепло. Поэтому первый и третий интегралы равны соответственно
состоит температура резервуара, от которого тело получает тепло. Поэтому первый и третий интегралы равны соответственно
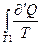 =
= 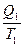 ;
; 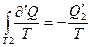 (18)
(18)
но Q 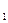 и Q
и Q 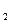 в (18) не совпадают с соответствующими величинами при обратимом цикле. Учитывая (16) и (18),получаем:
в (18) не совпадают с соответствующими величинами при обратимом цикле. Учитывая (16) и (18),получаем:
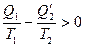
 или
или 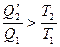 (19)
(19)
Следовательно,
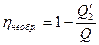
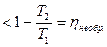 (20)
(20)
Что и требовалась доказать.
10.4. Термодинамические потенциалы
Расчеты в термодинамике выполняются с использованием функций состояния, называемых термодинамическими потенциалами.
Приращение каждого из потенциалов, в силу того, что он является функцией состояния, является полным дифференциалом некоторой функции, которой, собственно, данный потенциал выражается.
Полным дифференциалом функции 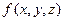 , по определению, называется величина:
, по определению, называется величина:
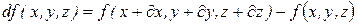 .
.
Эта величина определяется значениями 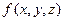 в начальной и конечной точках, а значит, не зависит от пути, по которому совершается переход между точками. Можно доказать, что полный дифференциал функции двух переменных
в начальной и конечной точках, а значит, не зависит от пути, по которому совершается переход между точками. Можно доказать, что полный дифференциал функции двух переменных 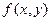 определяется выражением:
определяется выражением:
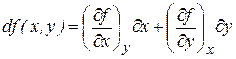 .
.
Поэтому, если полный дифференциал некоторой функции 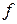 представлен в виде:
представлен в виде:
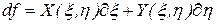 ,
,
где 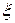 и
и 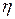 - параметры состояния системы (например, давление, объем, температура и т.п.), то можно утверждать, что
- параметры состояния системы (например, давление, объем, температура и т.п.), то можно утверждать, что 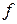 является функцией переменных
является функцией переменных 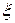 и
и 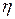 (их называют естественными переменными), а
(их называют естественными переменными), а 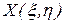 ,
, 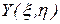 - ее частные производные. При этом:
- ее частные производные. При этом:
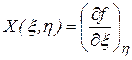
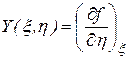
Приращение любого из потенциалов, поскольку они являются функциями состояния, равно полному, дифференциалу функции, которой он выражается.
Изменения термодинамических потенциалов, происходящие в ходе каких либо процессов, определяют либо совершаемую системой работу, либо получаемое работой тепло.
Одним из таких потенциалов является внутренняя энергия. На основе первого начала термодинамики для обратимых процессов можно записать соотношения:
dU = TdS – pdV
dU= 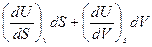 (21)
(21)
Из (21) получаем:
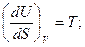
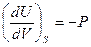 (22)
(22)
Поэтому S и V называют естественными переменными термодинамического потенциала U.
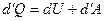
Если тело не обменивается теплом с внешней средой, то.
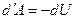 (23)
(23)
Таким образом, при отсутствии теплообмена с внешней средой работа равна убыли внутренней энергии тела.
При постоянном объеме
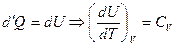 (24)
(24)
Другим термодинамическим потенциалом является свободнаяэнергия. Исходя из 1HT можем записать, что работа, производимая телом при обратимом изометрическом процессе,
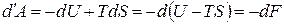 (25)
(25)
Функцию состояния,
F=U-TS (26)
Называют свободнойэнергией. Очевидно, что при обратимом изотермическом процессе работа равна убыли свободной энергии тела.
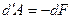 (27)
(27)
Таким образом, свободная энергия при изометрических процессах играет ту же роль, что и внутренняя энергия при адиабатических.
Дифференцируя (26), получаем:
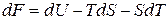 (26)
(26)
Подставим выражение для дифференциала 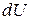 = TdS – pdV
= TdS – pdV
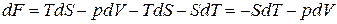
Таким образом, естественными переменными для свободной энергии являются температура и объем:
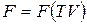
ЛЕКЦИЯ № 11. Кристаллическое и жидкое состояние вещества.
Элементы физической кинетики.
Дата добавления: 2015-09-14; просмотров: 942;
