Вязкость газов

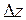Для понимания физических процессов, обеспечивающих вязкость газов, рассмотрим два соприкасающихся слоя газа толщиной , движущихся с различными скоростям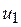и и . Каждая молекула этих слоев одновременно участвует в двух движениях: тепловом со средней скоростью 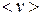и направленном со скоростью 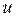, причем 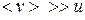. (Скорость теплового движения обычно бывает существенно больше скорости направленного, и мы ограничимся рассмотрением именно этого случая).

В результате теплового движения молекулы одного слоя переходят в другой и наоборот. Оценим количество молекул, пересекающих площадку S между слоями за время 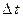в одном направлении в рамках модели, когда 1/6 часть молекул летит в заданном направлении. Площадку пересекают молекулы, которые к началу заданного промежутка времени 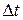находились в цилиндре с основанием S ивысотой в среднем 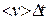, т.е.

. (11.11)

Произведем количественный расчет. Через площадку S в направлении оси 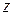за время 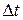переносится импульс:

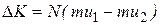(11.12)

Или, с учетом (11.11),

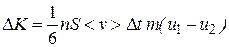(11.13)

Учтем, что в реальном газе скорость при переходе границы раздела между слоями изменится не скачком, а плавно, по некоторому закону 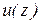. Логично считать, что каждая молекула переносит с собой импульс 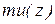, определяемый значением скорости 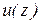в том месте, где произошло ее последнее столкновение перед переходом в новый слой. Естественно также положить, что в среднем последнее столкновение происходит на расстоянии, равном средней длине свободного пробега молекул l. Поэтому молекулам, летящим вдоль оси 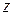, следует приписать скорость 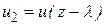, а в противоположном направлении 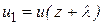. Учитывая, что l является малой величиной можно считать, что

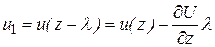
. (11.14)

Тогда разность скоростей молекул, совершивших встречные переходы между слоями

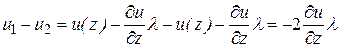. (11.15)

При этом импульс, который переносится молекулами через площадку S за время :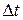

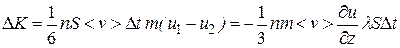(11.16)

Разделив на 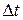, получим для потока импульса (количество через площадку в единицу времени):

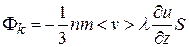(11.17)

Сравнивая соотношение (11.17) с эмпирическим уравнением (11.8):

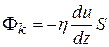
приходим к выводу о том, что (11.17) соответствует эмпирическому уравнению, если положить коэффициент внутреннего трения равным

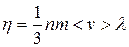(11.18)

Учтем, что произведение 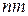дает плотность 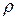газа, и окончательно получим выражение для коэффициент вязкости в рамках молекулярно-кинетической теории:

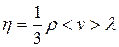(11.19)

Определим, как коэффициент внутреннего трения зависит от параметров газа. Для этого подставим в (11.19) выражения для входящих в него величин:

(11.20)

Из (11.20) видно, что 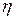зависит только от рода используемого газа (массы молекул, эффективного сечения молекул) и температуры, но не зависит от давления. Это можно легко объяснить. При уменьшении давления уменьшается плотность газа, но пропорционально растет средняя длина свободного пробега. При не очень низких давлениях эти две зависимости компенсируют друг друга.

Однако необходимо иметь в виду, что если давление станет настолько малым, что l превзойдет размеры сосуда, по которому протекает газ, то при дальнейшем уменьшении давления плотность газа будет уменьшаться, а l будет оставаться постоянной. В этих условиях зависимость h(р) будет наблюдаться.

Путем рассуждений, аналогичных проведенных нами для получения эмпирического уравнения вязкости на основе молекулярно-кинетических представлений, можно получить эмпирические уравнения диффузии (закон Фика) и теплопроводности (закон Фурье). При этом молекулярно-кинетическое выражение для коэффициента диффузии имеет вид:

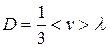(11.21)

А для коэффициента теплопроводности:

(11.22)

Очевидно, что между рассмотренными коэффициентами имеется простая связь:

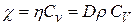(11.20)

Эта связь обусловлена аналогичностью физических процессов, происходящих при наблюдении трех указанных явлений переноса. Различие заключается в том, какая величина переносится между слоями газа.