Теоремы сложения вероятностей. а) Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
а) Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
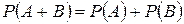 .
.
б) Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
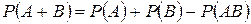 .
.
Замечание. Следует иметь в виду, что когда события образуют сумму, то они объединяются союзом “или” и наоборот.
в) Если события 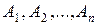 образуют полную группу, то сумма их вероятностей равна единице
образуют полную группу, то сумма их вероятностей равна единице
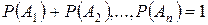 .
.
г) Принцип целесообразности применения противоположных событий: если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятности перейти к противоположному событию
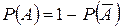 .
.
д) Исходя из того, что сумма событий состоит в появлении хотя бы одного из событий – слагаемых, в случае большого числа событий имеет смысл пользоваться другой формулой:
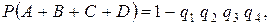
где 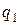 – вероятность непоявления
– вероятность непоявления  , т.е.
, т.е.  ,
,
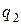 – вероятность непоявления
– вероятность непоявления 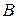 , т.е.
, т.е. 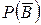 ,
,
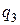 – вероятность непоявления
– вероятность непоявления 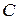 , т.е.
, т.е. 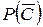 ,
,
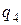 –вероятность непоявления
–вероятность непоявления 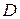 , т.е.
, т.е.  .
.
Дата добавления: 2015-10-13; просмотров: 642;
