Геометрическое определение вероятности
Вероятность равна отношению меры включаемого множества к мере включающего множества. Под мерой понимают длину, площадь или объем.
Свойства вероятности:
§ Вероятность достоверного события равна 1
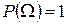 .
.
§ Вероятность невозможного события равна 0
Р(Æ) = 0 .
§ Вероятность случайного события принимает значения от нуля до единицы
 .
.
| Пример 1. | Подбрасывают игральную кость. Найти вероятность того, что выпавшее число очков окажется: а) четным; б) кратным 3. |
Решение.
У игральной кости 6 граней – это есть возможное число исходов.
а) Среди всех граней игральной кости имеется 3, содержащее четное число очков – 2,4,6. Поэтому вероятность будет равна:
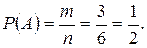
б) На гранях игральной кости есть два числа, кратных 3 – это 3 и 6. Поэтому вероятность будет равна
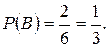
| Пример 2. | На карточках написаны буквы О, Р, Т, П, С. Какова вероятность, что при случайном раскладывании получится слово “СПОРТ”? |
Решение.
Число возможных исходов в данном случае равно числу перестановок, которое можно сделать из 5 букв, т.е. одно расположение букв отличается от другого расположения только порядком букв. Следовательно,
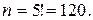
Благоприятный же исход всего один, и вероятность будет равна
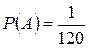 .
.
| Пример 3. | Абонент забыл две последние цифры номера телефона и помнит лишь, что они разные. Какова вероятность правильного набора номера? |
Решение.
Число возможных исходов равно числу размещений из 10 цифр по 2, т.к. могут участвовать любые две цифры, и при этом порядок набора тоже будет иметь значение. Итак,
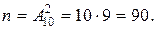
Благоприятный исход один, поэтому
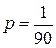 .
.
| Пример 4. | В группе студентов 15 девушек и 10 юношей. Отбирают команду из 5 человек. Какова вероятность, что в команде окажется 3 юноши? |
Решение.
Число возможных исходов равно числу сочетаний из 25 человек по 5 человек, т.к. каждый вариант команды отличается от другого хотя бы одним человеком, а порядок значения не имеет. Следовательно,
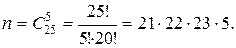
Подсчитаем число благоприятствующих исходов: среди 10 юношей выбирают 3-х, это можно сделать 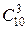 способами, остальные в команде – 2 девушки, их можно выбрать
способами, остальные в команде – 2 девушки, их можно выбрать 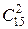 способами, причем каждый вариант выбора 3-х юношей может сочетаться с каждым вариантом 2-х девушек, поэтому число благоприятствующих исходов равно
способами, причем каждый вариант выбора 3-х юношей может сочетаться с каждым вариантом 2-х девушек, поэтому число благоприятствующих исходов равно 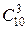
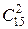 .
.
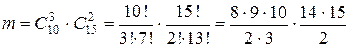 .
.
Искомая вероятность
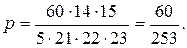
| Пример 5. | Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг квадрата. |
Решение.
Возможные исходы будут составлять точки круга, они заполняют площадь круга, т.е. 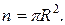 Чтобы определить благоприятствующие исходы, нужно найти площадь вписанного квадрата. Известно, что сторона квадрата, вписанного в круг радиуса
Чтобы определить благоприятствующие исходы, нужно найти площадь вписанного квадрата. Известно, что сторона квадрата, вписанного в круг радиуса 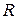 , равна
, равна 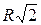 , тогда площадь его составляет
, тогда площадь его составляет 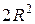 , т.е.
, т.е.
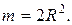
Вероятность равна
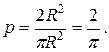
4. Основные теоремы и формулы
Как правило, для определения вероятностей событий применяются не только непосредственные прямые методы, а и косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных. Вся теория вероятностей, в основном, и представляет собой систему таких косвенных методов, применение которых позволяет свести необходимый эксперимент к минимуму.
Суммой двух событий  и
и 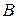 называют событие
называют событие 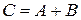 , состоящее в появлении хотя бы одного из событий
, состоящее в появлении хотя бы одного из событий  и
и 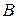 (или
(или  , или
, или 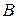 , или
, или  и
и 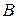 ).
).
Дата добавления: 2015-10-13; просмотров: 919;
