Аксиомы теории вероятностей

Вероятность события А обозначается P(A) или P{A}. Вероятность выбирают так, чтобы она удовлетворяла следующим условиям или аксиомам:

P(Ω) = 1; P( 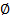) = 0 (2.1)

P( 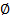) ≤ P(A) ≤ P(Ω) (2.2)

Если A_i и A_j несовместные события, т. е. A_i ∩ A_j = 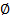, то

P(A_i 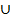A_j) = P(A_i) + P(A_j), (2.3)

где 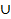- знак логического сложения событий, 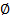– пустое множество (отсутствие событий).

Аксиома (2.3) обобщается на любое число несовместных событий {А_i}ⁿⁱ = 1:

(2.4)

Частотное определение вероятности любого события А:

P(A) = m_A / n (2.5)

представляет отношение числа случаев (m_A), благоприятных появлению события А, к общему числу случаев (возможному числу исходов опыта) n.

При неограниченном возрастании числа n наблюдается статистическое упорядочение, когда частота события А (выборочная оценка) все меньше изменяется и приближается к постоянному значению - вероятности события А.