АКСИОМЫ

1. Правила получения значения младшего разряда суммы одноразрядных десятичных чисел:

0 + 0 = 0 , . . . , 0 + 9= 9;

1+1= 1 , . . . , 1 + 9 = 0;

9 + 0 = 9 , . . . , 9 + 9 = 8.

2. Правила получения значения переноса в старший разряд при сложении двух одноразрядных чисел (если сумма таких чисел одноразрядная, то считаем его равным 0):

0 + 0 = 0s, . . . , 0 + 9= 0s;

1+1= 0s, . . . , 1 + 9 = 1s;

9 + 0 = 0s, . . . , 9 + 9 = 1s.

Символs используется в приведенных продукциях для указания на то, что они определяют величину переноса.

3. Специальные аксиомы:

x + 0 = x;

x + y = y+x.

Эти аксиомы формулируются в предположении, что x и y представляют собой числа.

4. Продукция-неаксиома

Правило сложения двух десятичных чисел:

p = .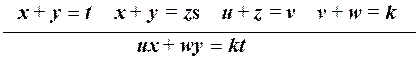

По последнему правилу можно найти сумму двух произвольных чисел, записываемых как ux и wy, где x и y - младшие разряды десятичных записей чисел, если выполнены (или вычислены) соотношения, являющиеся посылками продукции:

a) значение младшего разряда суммы равно t (может быть взято из соответствующей аксиомы);

б) значение переноса при сложении младших разрядов равно z (также берется из аксиомы);

в) значение суммы чисел u и w вместе со значением переноса z равно k.

Нетрудно видеть, что приведенные правила воспроизводят знания, используемые в общеизвестной процедуре поразрядного сложения десятичных чисел справа-налево.

Тогда соответствующая система Поста имеет вид
P= (A, B,V, P), где P - это приведенные продукции, а

A = { +, =, s, 0, . . . , 9}, B = Æ и V = { x, y, z, v, w, k, t}.

Заметим, что все продукции приведенной системы, за исключением одной, являются аксиомами, задающими простейшие соотношения, на основании которых можно воспользоваться основным правилом в продукции p. При этом продукция, соответствующая аксиоме x + y = y + x является избыточной.