СИСТЕМАХ

Выводы в системах Поста и множества выводимых слов обладают рядом интересных и важных свойств.

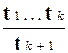1. Существует алгоритм, который по произвольным словам в основном и вспомогательном алфавитах ₁, . . . , _k, _k+1 и продукции p = определяет выводимость слова _k+1 из слов ₁, ... , _k с помощью продукции p.

Возможен следующий алгоритм определения применимости произвольной продукции p к заданным словам ₁, ... , _k.

1.1. Выделяются все различные символы переменных в образцах t₁, . . . , t_k+1.

1.2. Находится длина dсамого короткого слова среди слов ₁, ... , .

1.3. Для выделенного множества символов переменных строятся все подстановки, в которых эти переменные заменяются такими словами в основном и вспомогательном алфавитах, длина которых не превосходит d.

1.4. Для каждой подстановки Q проверяется условие:

"i = 1,. . . , k+1( _i = t_i Q) (1)

1.5. Если условие (1) имеет место хотя бы для одной подстановки, то _k+1 выводится из ₁, ... , _k с помощью продукции p.

1.6. Если для всех подстановок условие (1) не выполняется, то _k+1 не выводится из ₁, ... , _k с помощью p.

2. Существует алгоритм, который по произвольной последовательности ₁, . . . , _k - слов в основном и вспомогательном алфавитах заданной системы Поста P определяет, является ли эта последовательность выводом в P или нет.

Пример соответствующего алгоритма может быть получен на основе схемы предыдущего алгоритма.

3.Множество различных слов, которые могут быть получены из слов ₁, ... , _k применением продукции p = 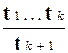является конечным.