Вычисление теоретического
Ряда частот распределения Пуассона
Если известно, что случайная величина распределена по закону Пуассона и задано выражение этого закона, то возможным становится вычисление теоретических частот по формуле 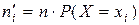 ,
, 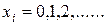
Значение функции Пуассона  находят по таблице
находят по таблице
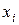
| 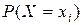
| 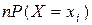
| 
| 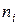
|
| 241,7 | ||||
| 0,3432 | 343,2 | |||
| 0,2437 | 243,7 | |||
| 0,1154 | 115,4 | |||
| 0,0409 | 40,9 | |||
| 0,0116 | 11,6 | |||
| 0,0028 | 2,8 | |||
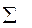
| 0,9993 |
Критерии согласия. Основные понятия
В предшествующих примерах закон распределения считался известным или существовали довольно веские основания для предположения о форме закона распределения по данному эмпирическому материалу. Сравнение фактических и вычисленных теоретических частот указывает на их близость, но полной сходимости нет. Между 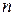 и
и 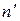 есть определенные, иногда довольно значительные расхождения. Отклонение фактических частот от теоретических можно объяснить с помощью двух утверждений:
есть определенные, иногда довольно значительные расхождения. Отклонение фактических частот от теоретических можно объяснить с помощью двух утверждений:
1. Эмпирические и теоретические частоты не противоречат одна одной, а расхождения между ними необходимо считать случайными, поскольку выбор элементов исследование проводили случайным способом. Сделанное предположение о распределении признака по теоретическому закону следует признать верным.
2. Расхождения между теоретическими и эмпирическими частотами объяснить случайностью невозможно. Распределение признака по выбранному теоретическому закону необходимо признать ошибочным. Следует тщательнее изучить вариационный ряд и попробовать подобрать новый закон, который точнее учитывал бы особенности эмпирического материала.
Для выбора между этими двумя выводами применяют критерии согласия.
Критерием согласия называют правило проверки гипотезы о предположенном законе неизвестного распределения.
Рассмотрим некоторые из них.
Критерий согласия Пирсона 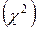
Пусть в результате наблюдений за случайной величиной 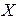 получено ее распределение в виде вариационного ряда, характеризуемого частотами
получено ее распределение в виде вариационного ряда, характеризуемого частотами  .
.
Их сумма – это объем совокупности 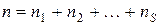 . Пусть эмпирическим частотам соответствуют теоретические
. Пусть эмпирическим частотам соответствуют теоретические  , сумма которых тоже равняется
, сумма которых тоже равняется 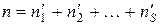 .
.
За меру расхождения теоретического фактического рядов частот Пирсон предложил взять среднее арифметическое квадратов отклонений соответствующих частот, разделенных на теоретические частоты
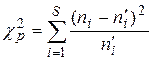 (1)
(1)
Если все фактические и теоретические частоты совпадают, то случайная величина 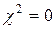 . В других случаях величина (1) отличается от нуля, и тем более, чем больше расхождения между
. В других случаях величина (1) отличается от нуля, и тем более, чем больше расхождения между 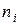 и
и 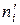 . По таблицам критических точек Пирсона находят точку
. По таблицам критических точек Пирсона находят точку 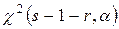 , где
, где 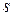 – это число групп (частичных интервалов) выборки;
– это число групп (частичных интервалов) выборки; 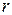 – число параметров теоретического распределения, которые было оценено по данным выборки,
– число параметров теоретического распределения, которые было оценено по данным выборки, 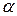 – уровень значимости, определяющий величину допустимой ошибки (0.1, 0.05, 0.01). В случае нормального распределения
– уровень значимости, определяющий величину допустимой ошибки (0.1, 0.05, 0.01). В случае нормального распределения 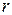 =2 (математическое ожидание и дисперсия), в случае распределения Пуассона
=2 (математическое ожидание и дисперсия), в случае распределения Пуассона 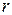 =1 (оценивают один параметр
=1 (оценивают один параметр 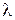 ).
).
Правило применение критерия Пирсона:
1. Вычислить по формуле (1) 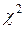
2. Найти по таблице 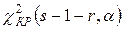
3. Сравнить фактическое и критическое значения 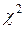
а) 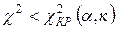 – нет оснований для отклонения выдвинутой гипотезы о теоретический закон распределения
– нет оснований для отклонения выдвинутой гипотезы о теоретический закон распределения
б) 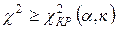 – гипотезу о законе распределения следует отклонить.
– гипотезу о законе распределения следует отклонить.
Для проверки правильности вычислений используют формулу
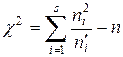 .
.
| Пример. | Проверить по критерию Пирсона выдвинутую гипотезу о нормальном распределении совокупности. |
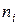
| |||||||||

|
Решение:
Вспомогательные вычисления удобно проводить в таблице
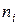
| 
| 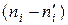
| 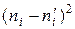
| 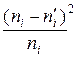
| 
| 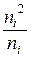
|
| 0,06 | 20,06 | |||||
| 0,01 | 113,01 | |||||
| -2 | 0,03 | 133,03 | ||||
| -1 | 0,01 | 103,01 | ||||
| 0,02 | 52,02 | |||||
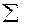
| 500,13 |
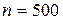
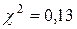
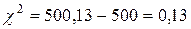
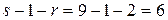
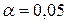
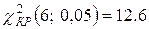
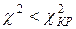 распределение выбрано верно.
распределение выбрано верно.
Эмпирические данные наблюдений согласованы с гипотезой о нормальном распределении генеральной совокупности.
Дата добавления: 2015-10-13; просмотров: 1398;
