Критерии согласия Ястремского

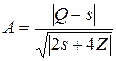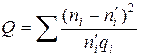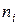Советский статистик Б.С.Ястремский доказал, что меру близости теоретического и фактического распределений можно характеризовать величиной , где , – эмпирические частоты, 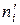– соответствующие теоретические частоты, , 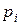– теоретическая вероятность того, что случайная величина 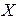примет значение ; 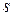– число групп; 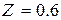при .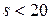

§ Если 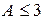, то расхождение между теоретическим и фактическим распределениями несущественно.

§ Если 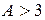, то это расхождение существенно и его невозможно объяснить влиянием случайных факторов, поэтому теоретический закон распределения следует отклонить.

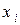
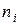
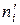
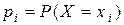
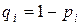
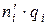
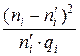
				0,2417	0,7583	183,5086	0,267
				0,3432	0,6568	225,2824	1,438
				0,2437	0,7563	184,5372	0,916
				0,1154	0,8846	101,729	0,157
				0,0409	0,9591	39,3231	0,025
				0,0116	0,9884	11,8608	3,035
				0,0028	0,9972	2,9916	0,334
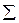
				0,9993			6,172

,

.

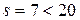
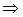
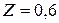
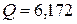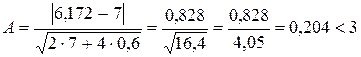Расхождение между теоретическим и фактическим распределениями несущественно. Гипотезу о распределении количества вызовов по закону Пуассона следует признать согласованной с экспериментом.