Критерий согласия Колмогорова
Пусть случайная величина 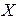 задана функцией распределения
задана функцией распределения 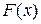 . По вариационному ряду вычисляют эмпирическую функцию распределения
. По вариационному ряду вычисляют эмпирическую функцию распределения 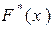 и определяют максимальное значение выражения
и определяют максимальное значение выражения 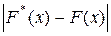 , которое обозначают через
, которое обозначают через 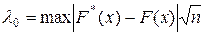 . Случайная величина
. Случайная величина 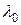 имеет распределение Колмогорова. По таблице находят вероятность
имеет распределение Колмогорова. По таблице находят вероятность 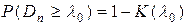 , где
, где 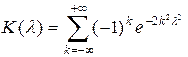 .
.
§ Если вероятность 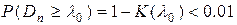 , то гипотезу о теоретическом законе распределения отвергают.
, то гипотезу о теоретическом законе распределения отвергают.
§ Если 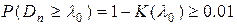 , то расхождения между
, то расхождения между 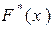 и
и 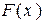 несущественны и гипотезу о теоретическом законе распределения следует считать согласованной с экспериментом.
несущественны и гипотезу о теоретическом законе распределения следует считать согласованной с экспериментом.
§ Если 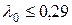 , то
, то 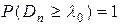 .
.
| Пример. | Проверить по критерию Колмогорова выдвинутую гипотезу о нормальном распределении роста взрослых мужчин. |
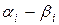
| 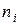
| 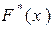
| 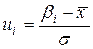
| 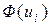
| 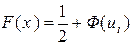
| 
|
| Менее 168 | –3,03 | –0,4988 | 0,0012 | 0,0012 | ||
| 168-170 | 0,008 | –2,35 | –0,4906 | 0,0094 | 0,0014 | |
| 170-172 | 0,046 | –1,66 | –0,4515 | 0,0485 | 0,0025 | |
| 172-174 | 0,16 | –0,98 | –0,3365 | 0,1635 | 0,0035 | |
| 174-176 | 0,384 | –0,29 | –0,1141 | 0,3859 | 0,0019 | |
| 176-178 | 0,654 | 0,39 | 0,1517 | 0,6517 | 0,0023 | |
| 178-180 | 0,862 | 1,08 | 0,3599 | 0,8599 | 0,0021 | |
| 180-182 | 0,964 | 1,76 | 0,4608 | 0,9608 | 0,0032 | |
| 182-184 | 0,994 | 2,45 | 0,4929 | 0,9929 | 0,0011 | |
| 184-186 | 3,13 | 0,4992 | 0,9992 | 0,0008 |
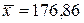 ,
,  . Наибольшее отклонение
. Наибольшее отклонение 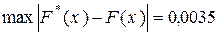 .
. 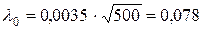 . Поскольку
. Поскольку 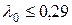 , то
, то 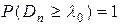 . Следовательно, данные очень хорошо согласованы с предположением о распределении роста взрослых мужчин по нормальному закону.
. Следовательно, данные очень хорошо согласованы с предположением о распределении роста взрослых мужчин по нормальному закону.
Дата добавления: 2015-10-13; просмотров: 1256;
