Алгебраический критерий Гурвица.
Алгебраические критерии устойчивости позволяют судить об устойчивости системы по коэффициентам характеристического уравнения.
Система автоматического регулирования устойчива, если все коэффициенты её характеристического уравнения имеют одинаковые знаки, а главный диагональный определитель системы (определитель Гурвица) и его диагональные миноры будут положительными.
Пусть 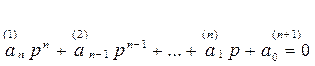 – характеристическое уравнение системы;
– характеристическое уравнение системы;
1) Необходимые условия: α0 > 0, α1 > 0,……, αn > 0 или α0<0, α1<0,….., αn<0.
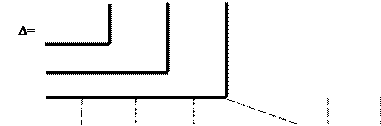
2) Для проверки достаточного условия, составляют из коэффициентов уравнения главный диагональный определитель:
- по главной диагонали определителя слева направо выписывают все коэффициенты характеристического уравнения, начиная со второго.
- столбцы вверх от главной диагонали дополняют коэффициенты с последовательно убывающими индексами;
столбцы вниз – коэффициентами с последовательно возрастающими индексами;
- iый диагональный минор получают отчёркивая iый столбец и iую строку.
Для исследуемой системы:
 |
| αn-1 | αn-3 | αn-5 | |||||
| αn | αn-2 | αn-4 | |||||
| αn-1 | αn-3 |
| |||||
| α1 | 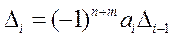 0 0
| ||||||
| α0 |
| C1 | C3 |
| C4 | C2 |
D1= αn-1>0;
| αn-1 | αn-3 |
| αn | αn-2 |
D2= = αn-1 αn-2 - αn αn-3 >0;
| αn-1 | αn-3 | ||
| αn | αn-2 | ||

| |||
| α0 |
| αn-1 | αn-3 | αn-5 |
| αn | αn-2 | αn-4 |
| αn-1 | αn-3 |
D3= >0; Dn= >0;
Исходным выражением для определения устойчивости по Гурвицу является Н(р), следовательно, по Гурвицу определяют устойчивость замкнутых и разомкнутых систем.
Пример 1. Определить по Гурвицу устойчивость системы первого порядка, заданной характеристическим уравнением:
Н(р)=α1р+α0=0
1)α1 >0; α0 >0
2)D=| α0| >0, т.е. для того, чтобы система первого порядка была устойчива, необходимо и достаточно, чтобы все коэффициенты её характеристического уравнения имели одинаковые знаки.
Пример 2. Определить по Гурвицу устойчивость системы второго порядка заданной характеристическим уравнением:
Н(р)=а2р2+α1р+α0=0
1)α1> 0; α2>0; α0>0
| α1 | |
| α2 | α0 |
2)D2= = α1 α0 – α2 0 >0
т.е. для того чтобы система второго порядка была устойчива, необходимо и достаточно, чтобы все коэффициенты её характеристического уравнения имели одинаковые знаки.
Пример 3. Определить по Гурвицу устойчивость замкнутой системы, заданной следующей структурной схемой:
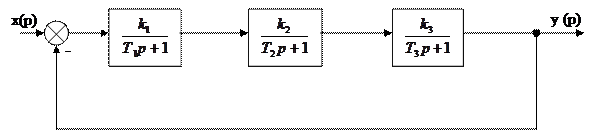 |
Исходным выражением для определения устойчивости по Гурвицу является характеристическое уравнение замкнутой САР, которое находится как знаменатель ее передаточной функции.
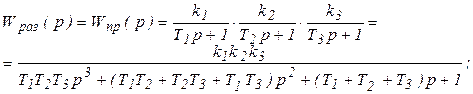
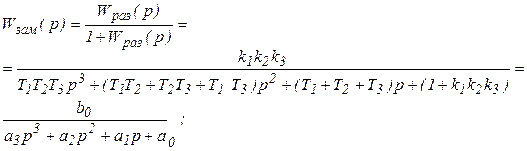
где: 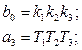
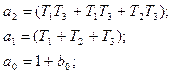

Первое условие: 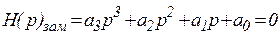
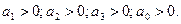
| а2 | а0 | |
| а3 | а1 | |
| а2 | а0 |
Второе условие:  ∆ =
∆ =
∆1 = α2 >0, если выполняется первое условие;
| α2 | α0 |
| α3 | α1 |
∆2= = α2 α1 - α3 α0 >0, в этом случае система устойчива;
∆3 = (-1)3+3 α0 ∆2>0 всегда, если α2>0 и выполняется первое условие.
Для того, чтобы система третьего порядка была устойчива, необходимо и достаточно, чтобы все коэффициенты ее характеристического уравнения имели одинаковые знаки, а произведение внутренних коэффициентов было больше произведения крайних.
Но может оказаться, что D2<0, тогда система неустойчива, и ее необходимо скорректировать, не прибегая к структурной коррекции. Это, возможно меняя статический коэффициент передачи разомкнутой САР. Для данной системы kраз = b0, а коэффициент характеристического уравнения α0=f(kраз).
В этом случае находят критическое значение kраз, при котором система находится на границе устойчивости, т. е. ∆2=0.
∆2= α2 α1 - α3 α0 кр=0
α0 кр= α2 α1/α3
kраз кр (для данной системы)= α0 кр - 1
Выбирают kраз ск < kраз кр и α0 ск = 1+ kраз ск
∆2 скор. сист. α2 α1 - α3 α0 ск >0, т. е. скорректированная система устойчива.
Дата добавления: 2015-09-28; просмотров: 1789;
