Частотный критерий Найквиста.

Этот критерий позволяет судить об устойчивости замкнутых САР по амплитудно-фазовой характеристике разомкнутой САР.

Замкнутая САР устойчива, если устойчива разомкнутая САР и её АФЧХ не охватывает точки с координатами (-1, j0)

Пусть W_раз=N(p)/M(p), тогда К(jω)_раз=N(jω)/M(jω) - выражение для АФЧХ. Построим АФЧХ разомкнутой САР.

Пусть АФЧХ проходит через точку (-1, j0). Что это значит?

Пусть на выход разомкнутой САР подан сигнал x_вх=Аsinωt. При некоторой частоте ω, К(jω1)=-1=1е^-jπ, т.е. амплитуда сигнала на выходе системы равна амплитуде на входе. Далее: Отрицательная обратная связь сдвигает фазу колебаний на –π, кроме того, сама система сдвигает фазу колебаний на –π, т.е. общий сдвиг равен 2π.Входные и выходные колебания в фазе. Если замкнуть теперь САР, то выходные колебания совпадут с выходными. Входные можно отключить, а в системе всё равно останутся незатухающие колебания. Следовательно, САР находится на границе устойчивости.

Пусть К_об(jω)=A_об е^jφоб

К_рег(jω)=A_рег е^jφрег

тогда К_раз(jω)= К_об(jω)·К_рег(jω)=-1,

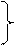т.е А_об · А_рег = 1

φ_об + φ_рег = - π условие возникновения незатухающих колебаний

Если же АФЧХ охватывает точку (-1, j0), то при этом

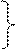А_об · А_рег >1

φ_об + φ_рег = -π

и следовательно, возникнут расходящиеся колебания.

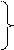Если же А_об · А_рег <1

φ_об + φ_рег = -π , т.е АФЧХ не охватывает точку (-1, j0), в системе возникают затухающие колебания и система устойчива.