Частотный критерий Михайлова.

Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик.

Пусть характеристическое уравнение системы имеет вид:

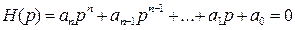(1)

Заменив в Н(р) оператор р на оператор jω, получим вектор Н(jω)

Пусть p₁, p₂,......, p_n - корни характеристического уравнения. Тогда в соответствии с теоремой Безу характеристическое уравнение (1) можно переписать в виде:

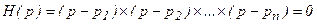или

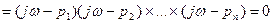Н(jω) (2)

Величина (jω-p_j) геометрически изображается векторами в комплексной плоскости, а Н(jω) представляет собой вектор, равный произведению элементарных векторов (jω-p_i), модуль этого вектора равен произведению модулей элементарных векторов, а фаза – сумма фаз элементарных векторов.

Условимся считать вращение против часовой стрелки положительным, тогда при изменении ω от 0 до ∞ каждый элементарный вектор повернется на некоторый угол.

Пусть p₁ - отрицательный действительный корень (“левый”, т. е. слева от мнимой оси), равный “ -α ₁”. При изменении ω от 0 до ∞

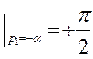arg(jω- p₁)

т. е. каждый “левый” действительный корень характеристического уравнения поворачивает вектор характеристического уравнения в комплексной плоскости при изменении ω от 0 до ∞ на угол 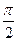в положительном направлении.

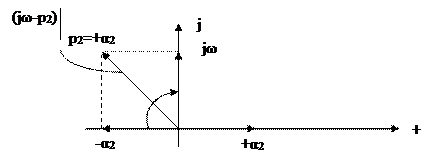
Если p₂ - положительный действительный корень (“правый”), равный “+α₂”,то при изменении ω от 0 до ∞

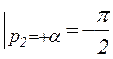arg(jω- p₂)

т. е. каждый “правый” действительный корень характеристического уравнения поворачивает вектор характеристического уравнения в комплексной плоскости при изменении ω от 0 до ∞ на угол 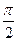в отрицательном направлении.

Если p_3,4 - корени комплексно-сопряженные с отрицательной действительной частью, равные –α₃ ± jβ₃, то

при изменении ω от 0 до ∞

arg(jω- p₃) (jω- p₄)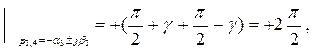

т. е. пара комплексно-сопряженных корней с отрицательной действительной частью поворачивает вектор характеристического уравнения в комплексной плоскости при изменении ω от 0 до ∞ на угол +2(π/2).

Если p_5,6 - комплексно-сопряженные корни с положительной вещественной частью, равные +α₄ ± jβ₄, то при изменении ω от 0 до ∞

arg(jω- p₅) (jω- p₆)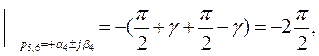

т.е. пара комплексно-сопряжённых корней с положительной действительной частью поворачивает вектор характеристического уравнения в комплексной плоскости при изменении ω от 0 до ∞ на угол 2π⁄2 в отрицательном направлении.

Анализируя выше изложенные случаи, можно сделать вывод:

Если система устойчива - все корни левые, и каждый даёт поворот на +π⁄2. Произведение векторов (jω-p_i)- тоже вектор. При изменении ω от 0 до ∞ его конец описывает кривую, называемую годографом Михайлова.

Следовательно, если все корни левые, угол поворота вектора характеристического уравнения (вектор Михайлова) равен сумме углов поворота векторов (jω-p_i), который в свою очередь равен +nπ⁄2. Если же хоть один корень правый, угол поворота вектора Михайлова меньше nπ⁄2, где n- порядок характеристического уравнения.

Таким образом, критерий Михайлова формулируется так:

САР устойчива, если при изменении ω от 0 до ∞ годограф Михайлова проходит последовательно n квадрантов, не обращаясь в 0, или САР устойчива, если при изменении ω от 0 до ∞ вектор Михайлова поворачивается на угол nπ⁄2 в положительном направлении, где n- порядок характеристического уравнения.

Годограф устойчивых систем

При увеличении статического коэффициента передачи разомкнутой САР, коэффициент а₀ растёт и годограф смещается вправо, параллельно самому себе. При некотором а_{0 кр} годограф проходит через начало координат. Это граница устойчивости. Очевидно а_{0 кр}=АВ, т.е. отрезку действительной оси, отсекаемому годографом Михайлова.