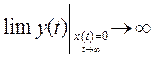Физическое и математическое определение устойчивости.

Система автоматического регулирования называется устойчивой, если после снятия возмущающего воздействия, которое вывело её из состояния равновесия, она вновь возвращается в состояние равновесия. Если система не возвращается в состояние равновесия после снятия возмущения, она неустойчива.

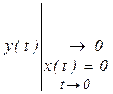
устойчивая система (кривые 1, 2)

неустойчивая (3).

Для определения математического условия устойчивости САР необходимо решить дифференциальное уравнение системы, когда правая часть этого уравнения равна 0 (при снятии возмущающего воздействия),и посмотреть, как ведет y_вых (t)при t ® ¥.

Пусть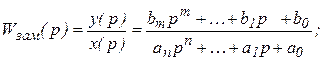

Тогда дифференциальное уравнение системы в операторной форме:

α_npⁿy(p) + ... + α₁py(p) + α_oy(p) = b_mp^mx(p) + ... + b₁px(p) + b_ox(p)

Оригинал дифференциального уравнения:

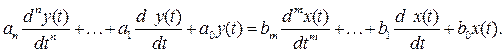
Для определения устойчивости системы, описываемой этим уравнением, снимем возмущения x(t)=0 и решим уравнение:

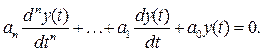
Для этого запишем характеристическое уравнение:

H(p) = α_npⁿ + .... + α₁p + α_o = 0.

Как видно из последнего выражения, характеристическое уравнение звена или системы – это знаменатель передаточной функции звена или системы, приравненный к нулю.

Если p₁, p₂, ..., p_n – корни характеристического уравнения, то решение этого уравнения имеет вид:

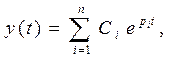где C_i – постоянные интегрирования, определяемые из начальных условий.

Рассмотрим отдельные случаи решения дифференциального уравнения:

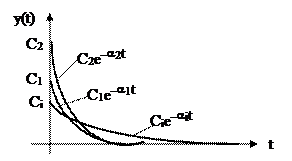1) p₁, p₂, ..., p_n – отрицательные действительные корни: p_i = -a_i. Решение уравнения в этом случае:

.

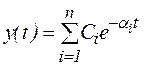2) p₁, p₂, ..., p_n - положительные действительные корни: p_i = +a_i.

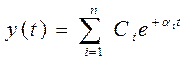– решение уравнения в этом случае

.

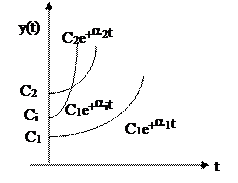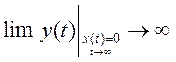3) p₁, p₂, ..., p_n - корни комплексно-сопряженные с отрицательной вещественной частью:

p_i = – a_i ± jb_i .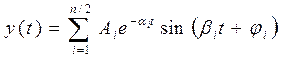

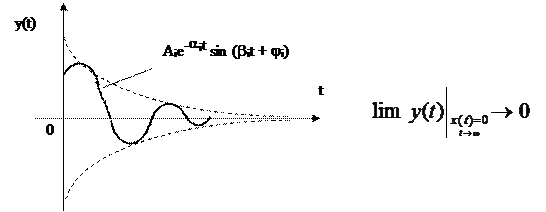4) p₁, p₂, ..., p_n – корни комплексно-сопряженные с положительной вещественной частью:

p_i = + a_i ± jb_i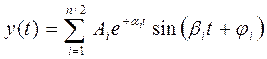

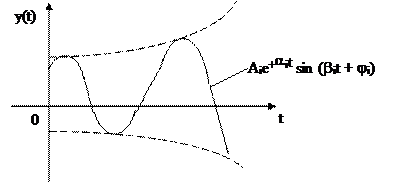Анализируя все случаи решения дифференциального уравнения для случая x(t) = 0, можно сделать вывод:

система автоматического регулирования устойчива, если все корни ее характеристического уравнения отрицательные действительные или комплексно-сопряженные с отрицательной действительной частью. Если же среди корней характеристического уравнения системы имеется хотя бы один положительный действительный корень или хотя бы одна пара комплексно-сопряженных корней с положительной вещественной частью, такая система неустойчива.

Математические правила, позволяющие определить знаки корней алгебраического (характеристического) уравнения, не решая это уравнение, в ТАУ называют критериями устойчивости.