Влияние этого звена на динамику системы рассмотрим на амплитудно–фазо–частотных характеристиках, исходной и скорректированной систем.

Пусть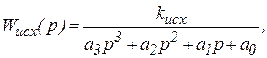

а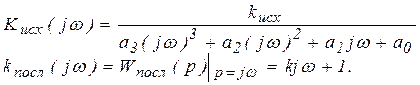

АФЧХ скорректированной системы получается путём перемножения АФЧХ исходной системы и АФЧХ корректирующего звена. Для получения АФЧХ скорректированной системы необходимо перемножить вектора исходной системы и корректирующего звена в комплексной плоскости на частотах от 0 до ¥ (при перемножении векторов в комплексной плоскости их модули перемножаются, а фазы складываются см. рис.)

Как видно из рисунка, АФЧХ скорректированной системы как бы повернулась против часовой стрелки, тем самым в скорректированной системе увеличился запас устойчивости по амплитуде и фазе.

Если p₁,p₂,p₃ – отрицательные действительные корни характеристического уравнения разомкнутой исходной системы, то её передаточная функция может быть записана в виде:

W_исх(Р) = ,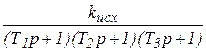

а переходная характеристика этой системы изображена на рисунке (кривая 1)

Пусть W_посл.1(р)=Т₁р+1, тогда

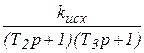W_ск.1(p)= , а

h_ск.1 – кривая 2.

W_посл.2(р)=Т₂р+1, тогда

W_ск.2(р)= 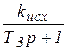, а h_ск.2-кривая 3.

W_посл.3(р)=Т₃р+1, W_ск.3(р)=К_исх (4)

Как видно из рисунка, последовательное корректирующее звено увеличивает быстродействие системы.