Преобразовательные элементы.

Корректирующие устройства систем регулирования осуществляют преобразование сигнала управления. С этой целью их составляют из элементов, которые удобно называть преобразовательными. Используются электрические, механические, гидравлические, пневматические и иные преобразовательные элементы.

Рассмотрим основные из них.

А. Пассивные четырёхполюсники.

Это электрически цепи из резисторов, конденсаторов и индуктивностей.

Общая схема пассивного четырёхполюсника имеет вид:

U₁- входное напряжение четырёхполюсника,

U₂- выходное напряжение четырёхполюсника.

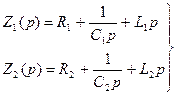- операторы сопротивления;

R_i , L_i , C_i – активные сопротивления, ёмкости и индуктивности;

Z_н – полное сопротивление нагрузки.

Если Z_н → ∞, то передаточная функция четырёхполюсника

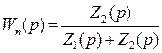
Варьируя вид операторов Z₁(p) и Z₂(p) и значения R_i , L_i , C_i можно получить большое количество четырёхполюсников, описываемых различными передаточными функциями. Стоимость пассивных четырёхполюсников низкая, а стабильность параметров достаточна высокая. Этими достоинствами объясняется и широкое использование в системах автоматического регулирования. Основной недостаток - ослабление сигнала.

Наиболее характерные схемы пассивных четырёхполюсников:

1)

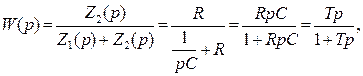
где T=RC. реальное дифференцирующее

2)

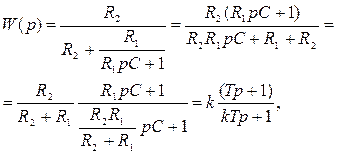
где k<1. (упругое с преобладанием дифференцирование)

3)

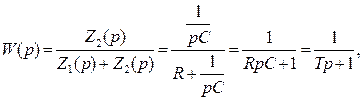
где T=RC – инерционное первого порядка

(реальное интегрирующее).

4)

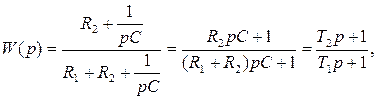
где T₂= R₁C

T₁= (R₁+R₁)C

- упругое, с преобладанием интегрирования.

Б. Активные четырёхполюсники.

Общая схема такого четырёхполюсника представлена на рисунке:

В активных четырёхполюсниках используется операционные усилители с очень большим коэффициентом усиления, поэтому передаточная функция четырёхполюсника с достаточной точностью равна:

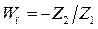
Активные четырёхполюсники удаётся выполнять так, что они осуществляют почти идеальное дифференцирование или интегрирование, тем более в ограниченном диапазоне частоты.

Например:

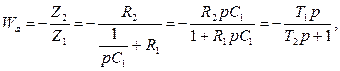
где T₁= R₂C₁; T₂= R₁C_1.

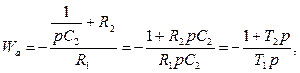
где T₂= R₂C₂; T₁= R₁C_2.