Нормального распределения
Для построения нормальной кривой существует два способа:
1. С помощью плотности вероятности
§ находят 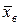 и
и 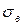 ;
;
§ находят теоретические частоты 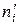 по формуле
по формуле 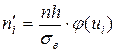 , где
, где 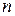 - сумма частот,
- сумма частот, 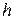 - разность между соседними вариантами,
- разность между соседними вариантами, 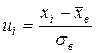 ,
, 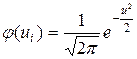 ;
;
§ строят точки 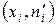 в прямоугольной системе координат и соединения их линией.
в прямоугольной системе координат и соединения их линией.
2. С помощью функции распределения
§ находят 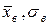 ;
;
§ находят теоретических частот 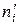 по формуле
по формуле 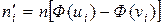 , где
, где 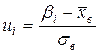 ,
, 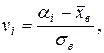
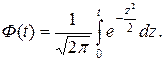
§ строят точки ( 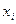 ,
, 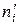 ) на координатной плоскости.
) на координатной плоскости.
| Пример. | Для предшествующего примера вычислить теоретический ряд частот с помощью плотности вероятности.
В качестве 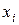 берут середины интервалов, берут середины интервалов, 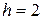 , , 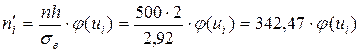
|
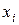
| 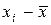
| 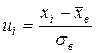
| 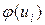
| 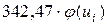
| 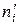
| 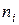
|
| –7,86 | –2,69 | 0,0107 | 3,66 | |||
| –5,86 | –2,01 | 0,0529 | 18,12 | |||
| –3,86 | –1,32 | 0,1669 | 57,16 | |||
| –1,86 | –0,64 | 0,3251 | 111,34 | |||
| 0,14 | 0,05 | 0,3984 | 136,54 | |||
| 2,14 | 0,73 | 0,3056 | 104,66 | |||
| 4,14 | 1,42 | 0,1456 | 49,86 | |||
| 6,14 | 2,1 | 0,0440 | 15,07 | |||
| 8,14 | 2,79 | 0,0081 | 2,77 | |||
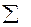
|
Сравнение теоретического ряда частот с эмпирическим распределением указывает на точность подобранного теоретического закона распределения.
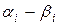
| 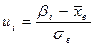
| 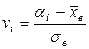
| 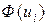
| 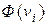
| 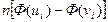
| 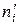
| 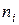
|
| 168-170 | –2,35 | –3,03 | –0,4906 | –0,4988 | 4,1 | ||
| 170-172 | –1,66 | –2,35 | –0,4515 | –0,4906 | 19,55 | ||
| 172-174 | –0,98 | –1,66 | –0,3365 | –0,4515 | 57,5 | ||
| 174-176 | –0,29 | –0,98 | –0,1141 | –0,3365 | 111,2 | ||
| 176-178 | 0,39 | –0,29 | 0,1517 | –0,1141 | 132,9 | ||
| 178-180 | 1,08 | 0,39 | 0,3599 | 0,1517 | 104,1 | ||
| 180-182 | 1,76 | 1,08 | 0,4608 | 0,3599 | 50,45 | ||
| 182-184 | 2,45 | 1,76 | 0,4929 | 0,4608 | 16,05 | ||
| 184-186 | 3,13 | 2,45 | 0,4912 | 0,4929 | 3,15 | ||
|
Если задан дискретный вариационный ряд, то нахождение теоретических частот с помощью плотности вероятности проводят на основе значений 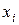 признака, а чтобы построить теоретический ряд с помощью функции распределения берут за основу такие интервалы, серединами которых являются наблюденные значения
признака, а чтобы построить теоретический ряд с помощью функции распределения берут за основу такие интервалы, серединами которых являются наблюденные значения 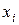 .
.
Дата добавления: 2015-10-13; просмотров: 971;
