Биноминальный закон распределения
Определение. Дискретная случайная величина Х имеет биноминальный закон распределения, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями
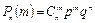 , ,
| (6.1) |
где 0 < р < 1, q = 1 – p, m = 0, 1, …, n.
Как видим, вероятности Р(Х = m) находятся по формуле Бернулли. Следовательно, биноминальный закон распределения представляет собой закон распределения числа X = m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.
Ряд распределения биноминального закона имеет вид:
| xi | … | m | … | n | |||
| pi | 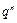
| 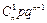
| 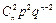
| … | 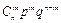
| … | 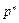
|
Теорема. Математическоеожидание случайной величины, распределенной по биноминальному закону
| M(X) = np, | (6.2) |
а ее дисперсия
| D(X) = npq. | (6.3) |
Следствие. Математическое ожидание частости события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью, равно
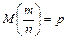 , ,
| (6.4) |
а ее дисперсия
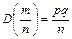 . .
| (6.5) |
Биноминальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях.
Дата добавления: 2015-11-10; просмотров: 2352;
