Взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин Х1, Х2, …, Хn, которые имеют одинаковые распределения, а следовательно, одинаковые характеристики (математическое ожидание, дисперсию и др.). Наибольший интерес представляют числовые характеристики среднего арифметического этих величин.
Обозначим среднее арифметическое n взаимно независимых случайных величин через 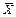 :
:
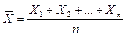 .
.
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 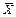 и соответствующими характеристиками каждой отдельной величины.
и соответствующими характеристиками каждой отдельной величины.
1. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
М( 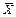 ) = а. ) = а.
| (5.32) |
2. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин:
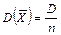 . .
| (5.33) |
3. Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в 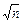 раз меньше среднего квадратического отклонения σ каждой из величин:
раз меньше среднего квадратического отклонения σ каждой из величин:
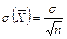 . .
| (5.34) |
Дата добавления: 2015-11-10; просмотров: 1678;
