Бесконечно малые величины

Последовательность 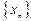называется бесконечно малой (б.м.), если .

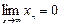Например,

, ,

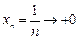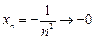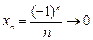
– бесконечно малые (условие 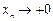означает, что 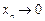, оставаясь положительной, а условие 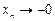означает, что 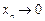, оставаясь отрицательной).

Функция a(х) называется бесконечно малой при х ® а, если .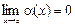

Например,

x, х², sin x, 1 – cos x, ln (1+x), e^x – 1

– бесконечно малые величины при х ® 0.

Пусть a(х) и b(х) – б.м. при х ® а. Тогда их сумма a(х) + b(х) и произведение a(х) · b(х) – б.м. при х ® а.

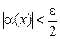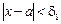Докажем, например, что a(х) + b(х) = g(х) – б.м. при х ® а. Пусть задано произвольное e > 0. Существует d₁ > 0 такое, что при (поскольку a – б.м. при х ® а). Далее, существует d₂ > 0 такое, что 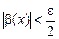при 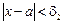(поскольку b – б.м. при х ® а). Положим 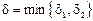. Тогда из условия 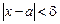следует, что .

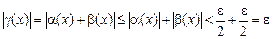Итак, для произвольного e > 0 мы указали d > 0 такое, что из условия 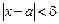следует, что 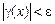. Это означает, что g = a + b – б.м. при х ® а. €

ЛЕММА. 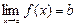тогда и только тогда, когда f(x) = b + a(x), где a(х) – б.м. при х ® а.

Докажите эту лемму самостоятельно, пользуясь определениями.