Предел функции на бесконечности. Горизонтальная асимптота

ЛЕКЦИЯ 3. ПРЕДЕЛЫ (Продолжение)

Предел функции на бесконечности. Горизонтальная асимптота

Сейчас мы определим, что означает стремление функции f(х) к величине b (f(х) ® b) при х ® + ¥, х ® – ¥, х ® ¥.

По определению, ,

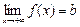если "e > 0 $М > 0 такое, что из условия х > М следует, что .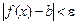

В этом случае говорят, что прямая у = b есть горизонтальная асимптота при х ® + ¥.

Определение предела 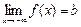аналогично предыдущему (надо лишь условие х > М заменить на условие х < – М. Нарисуйте картинку).

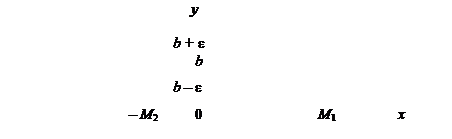
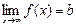Наконец, предел определяется так: "e > 0 $М > 0 такое, что неравенство 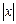> М влечет неравенство .

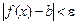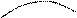
Говорят, что у = b – горизонтальная асимптота при х ® ¥.

Ниже мы рассматриваем предел 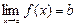, где а – число, либо + ¥, либо – ¥. Для определенности считаем, что а – число.

Можно ввести понятие «расширенной числовой прямой» ú, дополнив ú «бесконечно удаленной точкой» ¥, и определить окрестность точки ¥ как множество U_M (¥) (– ¥, – М) È (М, + ¥) при произвольном М > 0. Тогда в этих терминах понятие предела 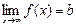можно сформулировать так: "e > 0 существует окрестность бесконечно удаленной точки U_M (¥) такая, что 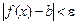"х Î U_M (¥).