Бесконечно большие и ограниченные величины, их связь с бесконечно малыми
Функция f(х) называется ограниченной на множестве А, если существует число М > 0 такое, что 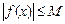 "х Î А (при этом, конечно, считаем, что f(х) определена на множестве, содержащем А).
"х Î А (при этом, конечно, считаем, что f(х) определена на множестве, содержащем А).
Пусть теперь w(х) определена в окрестности точки а за исключением, быть может, самой точки а. Функция w(х) называется ограниченной при х ® а, если существует окрестность U точки а и число
М > 0 такие, что 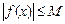 "х Î U, х ¹ а, т.е. f ограничена на U\{a}.
"х Î U, х ¹ а, т.е. f ограничена на U\{a}.
Например, функция 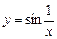 не определена в точке 0, но ограничена при х ® 0, поскольку
не определена в точке 0, но ограничена при х ® 0, поскольку 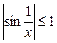 при х ¹ 0.
при х ¹ 0.
Пусть a(х) – б.м. при х ® а, а w(х) – ограниченная величина при х ® а. Тогда a(х) · w(х) – б.м. при х ® а, т.е.
| (б.м.) · огр. = б.м. |
Пример. 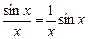 есть б.м. при х ® ¥, поскольку
есть б.м. при х ® ¥, поскольку 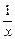 – б.м., а sin х – ограниченная (при х ® ¥).
– б.м., а sin х – ограниченная (при х ® ¥).
Последовательность 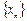 называется бесконечно большой (б.б.), если
называется бесконечно большой (б.б.), если 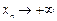 при п ® ¥. Например,
при п ® ¥. Например, 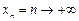 ,
, 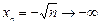 ,
, 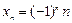 – б.б.
– б.б.
Функция f(х) называется б.б. при х ® а, если "N > 0 $d > 0 такое, что 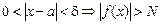 . Это определение дано для конечного а. Дайте соответствующие определения для а = + ¥ , – ¥, ¥.
. Это определение дано для конечного а. Дайте соответствующие определения для а = + ¥ , – ¥, ¥.
Если f(х) – б.б. при х ® а, то 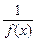 – б.м. при х ® а, т.е.
– б.м. при х ® а, т.е.
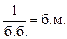
|
Если f(х) – б.м. при х ® а и f(х) ¹ 0 в окрестности точки а при
х ¹ а, то 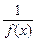 – б.б. при х ® а.
– б.б. при х ® а.
Другими словами,
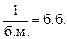 , (б.м. ¹ 0) , (б.м. ¹ 0)
|
Например, tg х – б.б. при 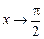 , а ctg х – б.м. при
, а ctg х – б.м. при 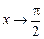 .
.
Дата добавления: 2015-09-14; просмотров: 1377;
