Бесконечно большие функции и их связь с бесконечно малыми
Определение. Предел функции  при
при 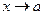 , где
, где 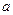 - число, равен бесконечности, если для любого числа
- число, равен бесконечности, если для любого числа 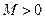 существует такое число
существует такое число 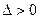 , что неравенство
, что неравенство
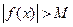
выполняется для всех  , удовлетворяющих условию
, удовлетворяющих условию
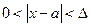 .
.
Обозначение: 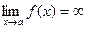 . Если в приведенном определении заменить условие
. Если в приведенном определении заменить условие 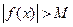 на
на 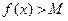 , то получим:
, то получим:
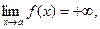
а если заменить на  , то:
, то:
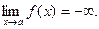
Графически приведенные выше случаи иллюстрируются следующим образом:
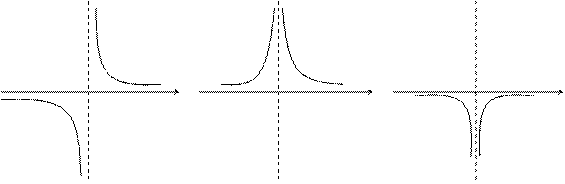 |
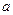

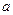

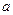

Определение. Функция называется бесконечно большойпри 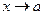 , где
, где 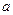 – число или одна из величин ¥, +¥ или -¥, если
– число или одна из величин ¥, +¥ или -¥, если 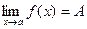 , где А–число или одна из величин ¥, +¥, -¥.
, где А–число или одна из величин ¥, +¥, -¥.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если 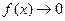 при
при 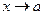 (
( 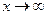 ) и не обращается в ноль, то
) и не обращается в ноль, то
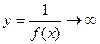 .
.
Дата добавления: 2015-09-29; просмотров: 1272;
