Бесконечно малые функции и их свойства
Определение. Функция  называется бесконечно малой при
называется бесконечно малой при 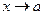 , где а может быть числом или одной из величин
, где а может быть числом или одной из величин 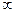 ,
, 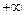 или
или 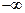 , если
, если 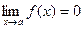 .
.
Бесконечно малой функция является только при указании к какому числу стремится аргумент  . При различных значениях
. При различных значениях 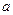 функция может быть бесконечно малой или нет.
функция может быть бесконечно малой или нет.
Пример. Функция 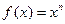 является бесконечно малой при
является бесконечно малой при 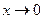 и не является бесконечно малой при
и не является бесконечно малой при 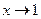 , т.к.
, т.к. 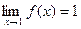 .
.
Теорема. Для того, чтобы функция  при
при 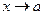 имела предел, равный А, необходимо и достаточно, чтобы в некоторой окрестностии точки
имела предел, равный А, необходимо и достаточно, чтобы в некоторой окрестностии точки 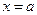 выполнялось равенство
выполнялось равенство
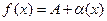 ,
,
где 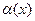 – бесконечно малая при
– бесконечно малая при 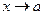 фунукция (
фунукция ( 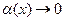 при
при 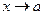 ).
).
Дата добавления: 2015-09-29; просмотров: 972;
