Предел функции в точке

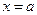Пусть функция определена в некоторой окрестности точки (т.е. в самой точке 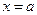функция может быть и не определена)

Определение. Число 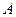называется пределом функции при 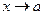, если для любого 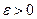существует такое число 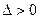, что для всех таких, что

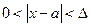
верно неравенство

.

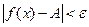То же определение может быть записано в другом виде:

Если 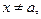то верно неравенство .

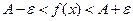Запись предела функции в точке: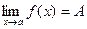

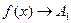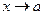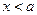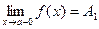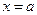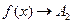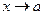Определение. Если при только при , то - называется пределом функции в точке слева, а если при только при 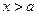, то 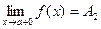называется пределом функции в точке 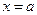справа.

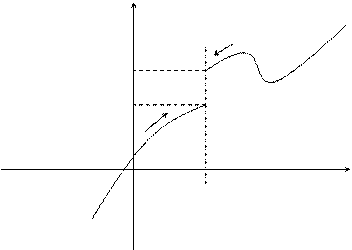
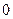
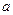
Приведенное выше определение относится к случаю, когда функция не определена в самой точке 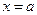, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы 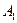и называются также односторонними пределами функции в точке 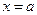. Также говорят, что 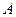– конечный предел функции .