Основные свойства функций. Функция с областью определения называется четной (нечетной), если для любого , выполняется равенство:

Функция 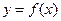с областью определения 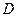называется четной (нечетной), если для любого 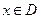, 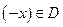выполняется равенство:

.

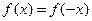
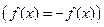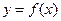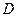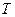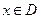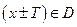Функция с областью определения называется периодической, если существует действительное число такое, что, если и , то

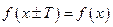
для любого .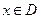

Наименьшее из таких чисел называется периодом функции .

Например, функции 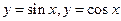являются периодическими с периодом 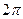, а функции 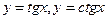- также периодические, но с периодом .

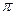Функция 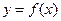называется возрастающей (убывающей) на множестве 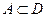, если для любых 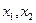из А таких, что 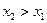, выполняется неравенство

.

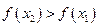
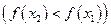Функция возрастающая (убывающая) на множестве А называется монотонной на этом множестве.

Пусть 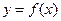- монотонная функция на множестве 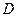и 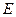- множество ее значений.

Функция 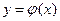с областью определения 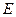называется обратной по отношению к функции 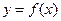, если для любого из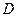

.

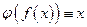Из этого определения следует, что график обратной функции 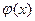получается симметрированием графика данной функции относительно биссектрисы 1^го и 3^го координатных углов.

Например, функци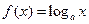й и 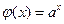– взаимно-обратные.

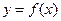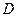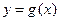Пусть - функция с областью определения , а - функция с областью определения 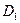. Обозначим через 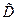множество тех значений аргумента , для которых 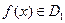. Тогда говорят, что на множестве 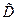определена сложная функция

.

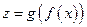Окрестностью точки называется всякий открытый интервал с центром в точке ; 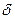- окрестностью точки называется интервал .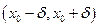

Пусть 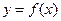- функция с областью определения 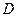. Точка 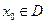называется точкой максимума (минимума), если существует 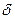-окрестность точки такая, что для всех из этой 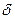-окрестности выполняются неравенства:

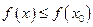
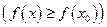
(от лат. maximum - наибольшее, minimum - наименьшее).

Точки максимума и минимума функции 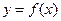называются точками экстремума (от лат. extremum - крайнее), а значения функции в этих точках - экстремумами функции.

В точках экстремума функция 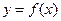меняет область своего возрастания (убывания) на область убывания (возрастания), т.е. в окрестности точки максимума график функции - «холм», а в окрестности точки минимума - «впадина».

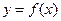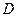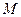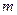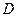
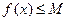
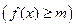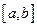Наибольшим (наименьшим) значением функции в области называется такое число (число ), что для всех из . Если функция задана на отрезке и ее график в каждой внутренней точке имеет единственную касательную, то наибольшее (наименьшее) значение функции на 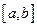есть максимальное (минимальное) из чисел , и значений функции во всех точках максимума (минимума) этой функции.