Свойства бесконечно малых функций

Сумма конечнонго числа бесконечно малых при 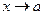функций является функцией бесконечно малой при .

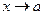Произведение конечного числа бесконечно малых при 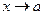функций является функцией бесконечно малой при .

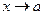Произведение бесконечно малой функции на функцию, ограниченную в некоторой окрестности точки 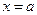является бесконечно малой функцией при .

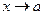Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.

Доказательство теоремы 2. Представим 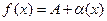, , 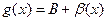где

, тогда

,

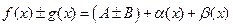где , 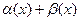– бесконечно малая функция. Следовательно

.

Теорема доказана.

Доказательство теоремы 3. Представим 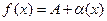, , 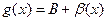где

, тогда

,

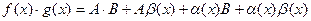где 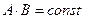, 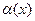и 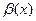– бесконечно малые. Следовательно,

.

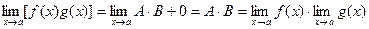Теорема доказана.