Основные теоремы о пределах

Теорема 1. 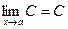, где С = const.

Следующие теоремы справедливы при предположении, что функции и и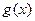меют конечные пределы при .

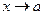Теорема 2.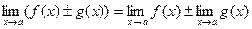

Теорема 3.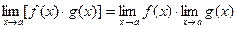

Следствие.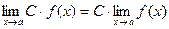

Теорема 4. 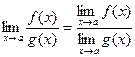при

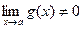
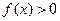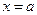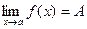Теорема 5. Если в некоторой окрестности точки и , то .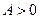

Аналогично определяется знак предела при .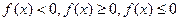

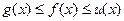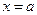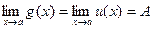Теорема 6. Если в некоторой окрестности точки и , то .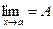

Определение. Функция называется ограниченной в некоторой окрестности точки 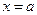, если существует такое числ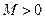о , что 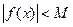для всех точек из этой окрестности.

Теорема 7. Если функция ) имеет конечный предел при 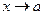, то она ограничена в некоторой окрестности точки .

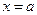Доказательство. Пусть 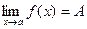, т.е. 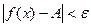, тогда

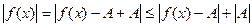или 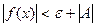, т.е. 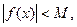где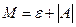

Теорема доказана.