Понятие функции. Способы задания функции
Функции. Предел функции
Понятие функции. Способы задания функции
Определение. Пусть 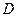 - произвольное множество действительных чисел:
- произвольное множество действительных чисел: 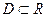 . Говорят, что задана функция
. Говорят, что задана функция 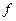 с областью определения D, если каждому числу
с областью определения D, если каждому числу  из множества D поставлено в соответствие единственное действительное число
из множества D поставлено в соответствие единственное действительное число 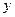 . Обозначение:
. Обозначение:
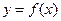 .
.
Читается: « 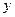 есть
есть 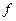 от
от  . Число
. Число  называется аргументом, число
называется аргументом, число 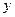 - значением функции
- значением функции 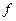 при данном значении
при данном значении  аргумента. Множество
аргумента. Множество  всех значений функции
всех значений функции 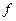 называется областью значений этой функции.
называется областью значений этой функции.
Определение. Графиком функции 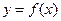 называется множество точек
называется множество точек  координатной плоскости, где
координатной плоскости, где  «пробегает» всю область определения
«пробегает» всю область определения 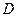 .
.
Основными способами задания функции являются: аналитический (т.е. с помощью формулы, выражающей 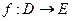 ), графический, табличный и словесный.
), графический, табличный и словесный.
При аналитическом задании функции обычно считается, что область ее определения совпадает с областью допустимых значений (ОДЗ) аргумента  в формуле
в формуле  . Например, областью определения функции
. Например, областью определения функции

является множество 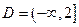 .
.
Примером словесного задания функции является функция Дирихле: 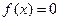 , если
, если  - иррациональное число,
- иррациональное число,  если
если  - рациональное число.
- рациональное число.
Заметим, что числовая последовательность - это функция с областью определения 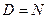 . В этом случае вместо
. В этом случае вместо 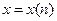 пишут просто
пишут просто  .
.
Дата добавления: 2015-09-29; просмотров: 634;
