Некоторые замечательные пределы

Отношение двух многочленов ,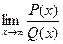

где 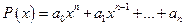, 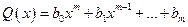- многочлены. Тогда

;

.

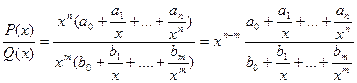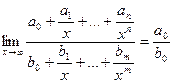Таким образом: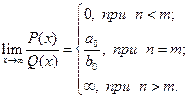

Первый замечательный предел .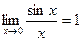

Второй замечательный предел .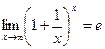

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:

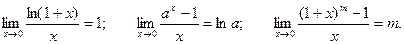
Пример. Найти предел.

.

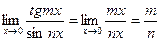Пример. Найти предел.

.

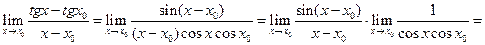
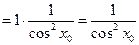Пример. Найти предел.

.

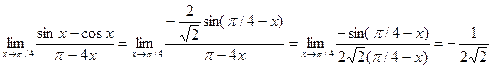Пример. Найти предел.

.

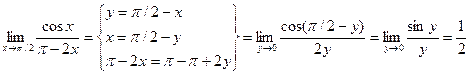Пример. Найти предел.

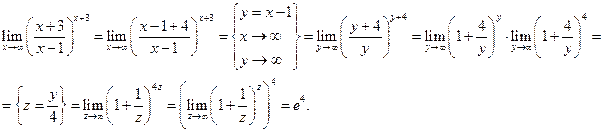
Пример. Найти предел .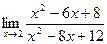

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.

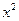– 6x + 8 = 0; 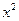– 8x + 12 = 0;

D = 36 – 32 = 4; D = 64 – 48 = 16;

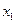= (6 + 2)/2 = 4; 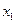= (8 + 4)/2 = 6;

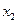= (6 – 2)/2 = 2 ; 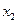= (8 – 4)/2 = 2;

Тогда 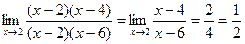ю

Пример. Найти предел. .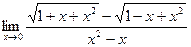

Домножим числитель и знаменатель дроби на сопряженное выражение: 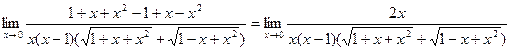= 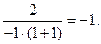Пример. Найти предел.

.

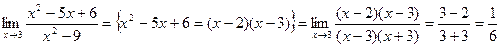Пример. Найти предел .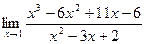

Разложим числитель и знаменатель на множители.

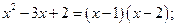
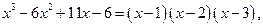так как

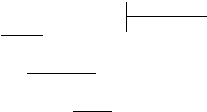x³ – 6x² + 11x – 6 x - 1

x³ – x² x² – 5x + 6

- 5x² + 11x

- 5x² + 5x

6x - 6

6x - 6 0

Следоваетльно,

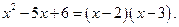
Тогда .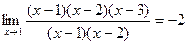

Пример. Найти предел.

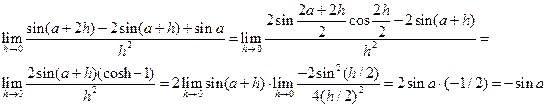
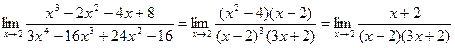- не определен, т.к. при стремлении к 2 имеют место различные односторонние пределы -∞ и +∞.