Свойства непрерывных функций. 1) Сумма, разность и произведение непрерывных в точке функций – есть функция, непрерывная в точке .

1) Сумма, разность и произведение непрерывных в точке функций – есть функция, непрерывная в точке .

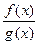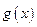2) Частное двух непрерывных функций – есть функция, непрерывная в точке , при условии, что не равна нулю в точке .

3) Композиция непрерывных в некоторой точке функций – есть функция непрерывная в этой точке

Это свойство может быть записано следующим образом:

Если 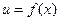, 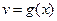– непрерывные функции в точке 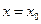, то функция 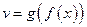– также непрерывная в этой точке.

Справедливость приведенных выше свойств можно доказать, используя теоремы о пределах функции в точке.