Свойства функций, непрерывных на отрезке
Свойство 1: (Первая теорема Вейерштрасса). Функция  , непрерывная на отрезке
, непрерывная на отрезке 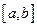 , является ограниченной на этом отрезке, т.е. сущестует такое положительное число
, является ограниченной на этом отрезке, т.е. сущестует такое положительное число 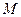 , что для всех
, что для всех 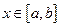 , выполняется неравенство
, выполняется неравенство 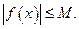
Свойство 2: (Вторая теорема Вейерштрасса). Функция  , непрерывная на отрезке
, непрерывная на отрезке 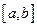 , достигает на нем свои наибольшее и наименьшее значения, т.е. существуют такие точки
, достигает на нем свои наибольшее и наименьшее значения, т.е. существуют такие точки 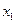 и
и 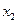 , принадлежащие отрезку
, принадлежащие отрезку 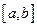 что
что 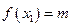 ,
, 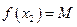 , и для всех
, и для всех 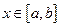 выполниется неравенство:
выполниется неравенство:
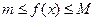
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например, функция 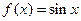 ).
).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебаниемфункции на отрезке.
Свойство 3: (Теорема Больцано – Коши). Функция  , непрерывная на отрезке
, непрерывная на отрезке 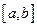 , принимает на этом отрезке все свои промежуточные значения, т.е. для любого числа
, принимает на этом отрезке все свои промежуточные значения, т.е. для любого числа 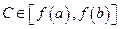 , существует точка
, существует точка 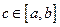 , такая, что
, такая, что 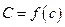 .
.
Свойство 4: Если функция  непрерывна в точке
непрерывна в точке 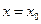 , то существует некоторая окрестность точки
, то существует некоторая окрестность точки  , в которой функция сохраняет определённы знак.
, в которой функция сохраняет определённы знак.
Свойство 5: (Вторая теорема Больцано – Коши). Если функция  - непрерывная на отрезке
- непрерывная на отрезке 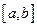 и принимает на концах этого отрезка значения противоположных знаков, то существует такая точка
и принимает на концах этого отрезка значения противоположных знаков, то существует такая точка 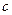 внутри этого отрезка, что
внутри этого отрезка, что 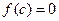 .
.
Определение. Функция  называется равномерно непрерывной на отрезке
называется равномерно непрерывной на отрезке 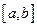 , если для любого
, если для любого 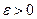 существует
существует 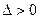 такое, что для любых точек
такое, что для любых точек 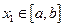 и
и 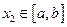 таких, что
таких, что
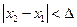
выполняется неравенство
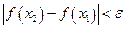 .
.
Отличие равномерной непрерывности от “обычной” в том, что для любого 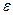 существует свое
существует свое 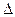 , не зависящее от
, не зависящее от  , а при “обычной” непрерывности D зависит от
, а при “обычной” непрерывности D зависит от 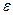 и
и  .
.
Свойство 6: (Теорема Кантора). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
Пример. 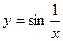 .
.
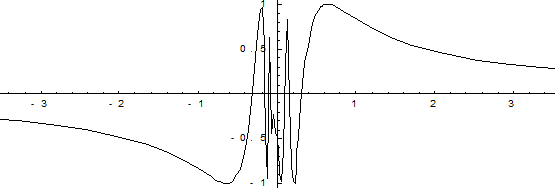
Функция 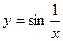 непрерывна на интервале
непрерывна на интервале 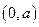 , но не является на нем равномерно непрерывной, т.к. существует такое число
, но не является на нем равномерно непрерывной, т.к. существует такое число 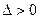 такое, что существуют значения
такое, что существуют значения 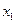 и
и 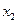 такие, что
такие, что 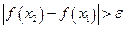 ,
, 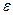 - любое число при условии, что
- любое число при условии, что 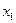 и
и 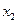 близки к нулю.
близки к нулю.
Свойство 7: Если функция  определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция
определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция 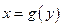 тоже однозначна, монотонна и непрерывна.
тоже однозначна, монотонна и непрерывна.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
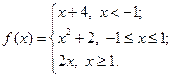
Имеем
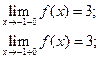
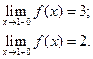
В точке 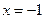 функция непрерывна; в точке
функция непрерывна; в точке 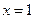 имеет разрыв 1 – го рода.
имеет разрыв 1 – го рода.
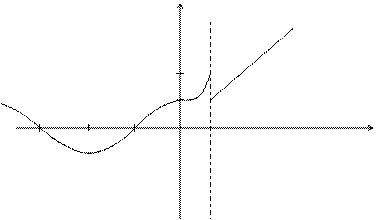
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
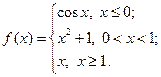
Имеем
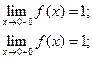
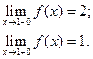
В точке 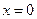 функция непрерывна; в точке
функция непрерывна; в точке 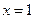 имеет разрыв 1 – го рода.
имеет разрыв 1 – го рода.
 |
у
-p -p/2 0 1 x
Дата добавления: 2015-09-29; просмотров: 850;
