Непрерывность некоторых элементарных функций

1) Функция 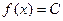, 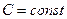– непрерывная функция на всей области определения.

2) Рациональная функция 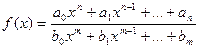непрерывна для всех значений , кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.

3) Тригонометрические функци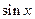и и 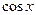непрерывны на своей области определения.

Докажем свойство 3) для функции .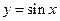

Запишем приращение функции

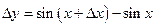, или .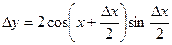

Тогда

.

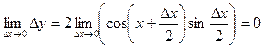Действительно, рассмотрим предел произведения двух функци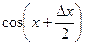й и 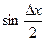. Функция косинус – ограниченная функция при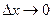 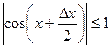, а так как

предел функции синус 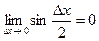, то она является бесконечно малой при .

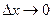Таким образом, имеем произведение ограниченной функции на бесконечно малую. Следовательно, это произведение, т.е. функция 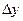– бесконечно малая. В соответствии с рассмотренными выше определениями, функция 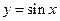– непрерывная функция для любого значения 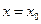из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.