Точки разрыва функции и их классификация. Рассмотрим некоторую функцию , непрерывную в окрестности точки , за исключением может быть самой этой точки

Рассмотрим некоторую функцию , непрерывную в окрестности точки , за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что 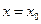является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Заметим, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел функции в точке при 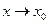справа существует и равен значению функции в этой точке, то функция называется непрерывной справа в точке . Обозначение: .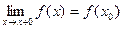

Если односторонний предел функции в точке при 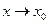слева существует и равен значению функции в этой точке, то функция называется непрерывной слева в точке . Обозначение: ..

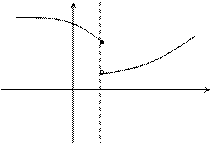Определение. Точка называется точкой устранимого разрыва функции , если в этой точке функция имеет конечные, равные друг другу левый и правый пределы, не равные значению функции в точке :

.

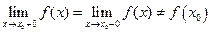При этом в самой точке функция может быть и не определена. Если доопрпеделить значение функции в точке 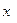положив его равным 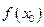, то функция будет непрерывной в точке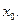

Определение. Точка называется точкой разрыва 1- го рода функции , если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы:

.

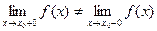Определение. Точка называется точкой разрыва 2 – го рода функции , если один из односторонних пределов функции в этой точке либо не существует либо равен бесконечности.

Пример. Функция Дирихле

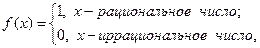
не является непрерывной в любой точке .

Пример. Функция 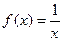имеет в точке 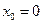точку разрыва 2 – го рода, т.к.

.

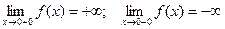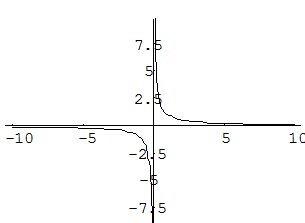
Пример. .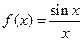

Функция не определена в точке 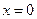, но имеет в ней конечный предел 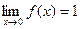, т.е. точка 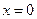является точкой устранимого разрыва функции . Если доопределить функцию в точке :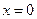

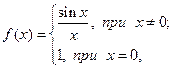
то функция будет непрерывной на всей числовой оси. График этой функции:

Пример. = .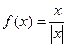

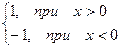y

0 x

-1

Эта функция обозначается как 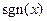– знак числа . В точке 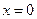функция не определена. Так как левый и правый пределы функции различны, то 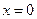-и точка разрыва 1 – го рода. Если доопределить функцию в точке 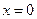, положив 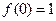, то функция будет непрерывна справа, если положить 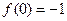, то функция будет непрерывной слева, если положить равное произвольному числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа. В этом случае будет иметь в точке 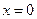разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.

Определение. Функция называется непрерывной на интервале (отрезке), если она непрерывна в каждой точке интервала (отрезка).

При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.