Первый замечательный предел

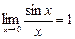
Другими словами, sin x ~ x при х ® 0. (Отметим, что этот предел есть неопределенность типа ).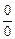

Доказательство вытекает из рассмотрения следующей картинки:

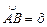Здесь радиус ОА = 1, дуга , катет АС = tg х. Имеем:

S_ªОАВ < S_{сектораОАВ} < S_ªОАС.

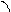Но S_ªОАВ = 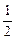ОА·ОВ·sin x = 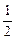sin x;

S_{сектораОАВ}= R²·x = 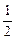x; S_ªОАC = 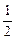ОА·AC = 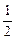tg x.

Итак, 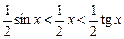. Из первого неравенства вытекает, что 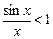, а из второго, что .

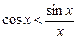Итак, 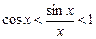. При этом cos x ® 1 при х ® 0.

Переходя к пределу в двойном неравенстве и пользуясь тем, что для предельных величин сохраняется нестрогое неравенство, получаем требуемую формулу. €

Таблица эквивалентностей

Существуют и другие эквивалентные б.м. Вот список некоторых из них:

при х ® 0

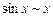
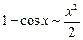
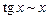
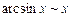
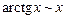
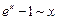
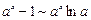
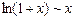
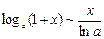
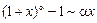, в частности,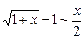

Как пользоваться этой таблицей?

Имеет место следующее

УТВЕРЖДЕНИЕ. Пусть a ~ a₁ и b ~ b₁ (где a, a₁, b, b₁ – б.м. при х ® а). Тогда

.

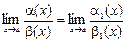Доказательство заключается в следующей простой выкладке:

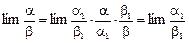
поскольку . €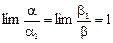

Итак, при вычислении пределов отношений б.м. величин можно эти б. малые заменять на эквивалентные б.м.

Пример. Вычислить предел .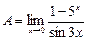

Поскольку 5х – 1 ~ xln 5, а sin 3x ~ 3x (при х ® 0), то

.

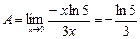Замечание. Подчеркнем, что данное правило о замене б.м. на эквивалентные б.м. при вычислении пределов относится только к отношениям б.м. , но не относится к суммам a + b и разностям
a – b; в последних двух случаях переход к эквивалентным б.м. при вычислении пределов может привести к ошибкам. Вот соответствующий пример. Найти предел 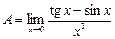. Если заменить в числителе tg x на х и sin x на х, то ответ будет ноль, что неверно. Правильное решение таково:

.

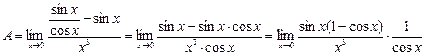Теперь уже можно воспользоваться тем, что 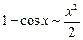, , 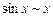поскольку мы имеем дело с отношением б.м. Учитывая также, что cos х ® 1 при х ® 0, получаем

.

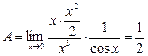В заключение определим, что означает запись b = О(a) (читается «бета есть О большое от альфа»), где a = a(х) и b = b(х) – б.м. при х ® а. Она означает, что существует константа С > 0 такая, что 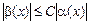для всех х из достаточно малой окрестности точки а, не совпадающих с а. Если b ~ a, то b = О(a), но обратное неверно.

Например, для 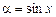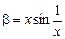имеем b = О(a), но при этом a не эквивалентно b.