V. Вывод формулы для определения момента инерции.
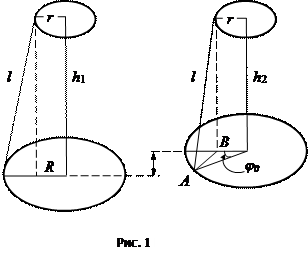
Пусть при вращении диск поднялся, на высоту h =h1 - h2 (рис. 1). Тогда приращение потенциальной энергии равно
.
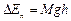При опускании нижнего диска потенциальная энергия переходит в кинетическую энергию вращательного движения
,
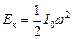где I0 - момент инерции нижнего диска, w - угловая скорость диска.
  |
В момент прохождения диском положения равновесия угловая скорость w, а, следовательно, и кинетическая энергия, принимает максимальное значение, т.е. w = w0 .
Если пренебречь трением, то на основании закона сохранения энергии для колеблющегося диска можно записать:
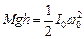. (2)
Угловая скорость w, являющаяся первой производной от смещения j по времени, может быть записана
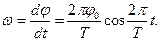
Максимальное значение угловой скорости равно:
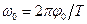. (3)
На основании выражений (2) и (3) имеем:
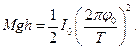(4)
Найдем величину h при повороте диска на малый угол j0, считая, что h1 + h2 » 2l:
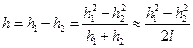. (5)
Из рис.1 ясно, что
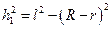и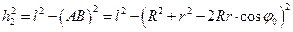 
.
Подставляя значение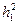 
и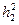 
в (5), получим:
.
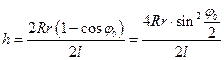Вследствие малости угла j0 синус можно заменить аргументом:
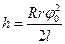. (6)
Подставив выражения (3) и (6) в формулу (2), получим:
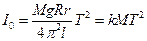, или
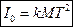, (7)
где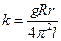 
- постоянная установки.
Дата добавления: 2015-09-11; просмотров: 2161;