Теоремы о пределах

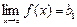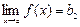1°.Единственность предела: если и , то .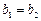

Доказательство проводится от противного.

Пусть 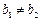. Положим 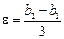. Тогда окрестност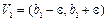и и 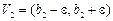не пересекаются.

Поскольку 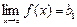, то для указанного e найдется d₁ > 0 такое, что неравенства 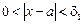влекут условие f(x) Î V₁.

Поскольку 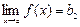, то для того же e найдется d₂ > 0 такое, что неравенства 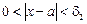влекут условие f(x) Î V₂.

Положим 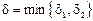. Тогда из неравенств 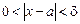должны следовать оба условия f(x) Î V₁ и f(x) Î V₂, что невозможно, поскольку V₁ Ç V₂ = Æ. Утверждение теоремы следует из полученного противоречия. €

Приведенное рассуждение – пример того, насколько тщательно математики следят за прочностью фундамента, на котором строится здание теории. С точки зрения «здравого смысла» доказываемое утверждение представляется очевидным. Однако случается, что «здравый смысл» подводит, и поэтому приходится соблюдать известную осторожность.

Тем не менее, в дальнейшем мы будем часто опираться именно на «здравый смысл», опуская большинство доказательств. Восстановить их вы сможете, читая известные руководства по математическому анализу.

Пусть для функций f и g в точке а существуют пределы

, .

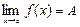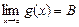Тогда справедливы утверждения:

2°. Предел суммы f + g существует и равен сумме пределов 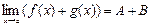. Или, коротко:

.

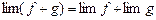3°. Предел произведения f · g существует и равен произведению пределов 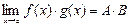, или

.

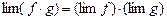4°. Предел частного 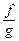существует и равен частному от пределов 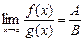при условии, что В ¹ 0. Другими словами,

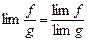, если lim g ¹ 0.

5°. Пусть f(х) £ g(х) в окрестности точки а. Тогда

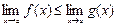
т.е. неравенство передается и предельным величинам.

6°. Теорема о пределе сложной функции:

пусть 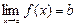и пусть 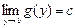. Тогда .

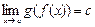Докажем для примера утверждение 2°, используя лемму и тот факт, что сумма бесконечно малых есть б.м. Имеем в силу леммы:

, ,

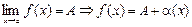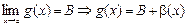где a и b – б.м. при х ® а. Тогда f(х) + g(х) = (А + В) + (a(х) + b(х)). Поскольку a + b – б.м. при х ® а, то отсюда снова в силу леммы получаем: 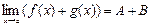, ч.т.д. €