Закон распределения Пуассона

Определение. Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, …, m с вероятностями

,

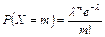(6.6)

где m = 0, 1, 2, ….

Ряд распределения закона Пуассона имеет вид:

xi				…	m	…
pi				…		…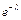

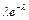
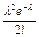
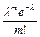
Теорема. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.

При достаточно больших n (вообще при n → ∞) и малых значениях р (р → 0) при условии, что произведение np – постоянная величина (nр → λ = const), закон распределения Пуассона является хорошим приближением биноминального закона. Т.е. при n → ∞, р → 0, nр → λ = const закон распределения Пуассона является предельным случаем биноминального закона. Так как при этом вероятность р события А в каждом испытании мала, то закон распределения Пуассона часто называют законом редких явлений.

По закону Пуассона распределены, например, число сбоев на автоматической линии, число отказов сложной системы в нормальном режиме, число требований на обслуживание в единицу времени в системах массового обслуживания, и т.п.

Отметим еще, что если случайная величина представляет собой сумму двух независимых случайных величин, каждая из которых распределена по закону Пуассона, то она также распределена по закону Пуассона с параметром

λ = λ₁ + λ₂.