Нормальный закон распределения

Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Определение. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и σ², если ее плотность вероятности f(x) имеет вид:

.

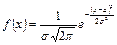(6.19)

Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 6.5 а), б) показана нормальная кривая с параметрами а и σ² и график функции распределения.

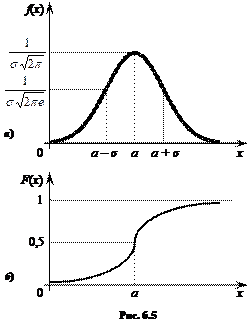Обратим внимание на то, что нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный 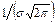, и две точки перегиба х = а 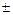σ с ординатами .

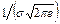Можно заметить, что в выражении плотности нормального закона параметры распределения обозначены буквами а и σ², которыми мы обозначали математическое ожидание и дисперсию. Такое совпадение не случайно. Рассмотрим теорему, которая устанавливает теоретико-вероятностный смысл параметров нормального закона.

Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру a этого распределения, т.е.

а ее дисперсия – параметру σ², т.е.

Выясним, как будет меняться нормальная кривая при изменении параметров а и σ.

Если σ = const, и меняется параметр a (а₁ < а₂ < а₃), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 6.6).

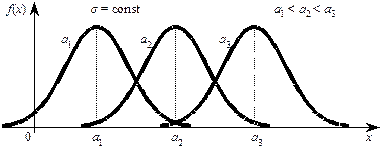
Рис. 6.6

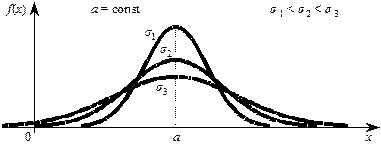
Рис. 6.7

Если а = const и меняется параметр σ, то меняется ордината максимума кривой f_max(a) = 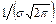. При увеличении σ ордината максимума уменьшается, но так как площадь под любой кривой распределения должна оставаться равной единице, то кривая становится более плоской, растягиваясь вдоль оси абсцисс. При уменьшении σ, напротив, нормальная кривая вытягивается вверх, одновременно сжимаясь с боков (рис. 6.7).

Таким образом, параметр a характеризует положение, а параметр σ – форму нормальной кривой.

Нормальный закон распределения случайной величины с параметрами a = 0 и σ = 1 называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.

Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, связана с тем, что интеграл от функции нормального распределения не выражается через элементарные функции. Однако его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения 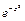или 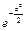. Такую функцию называют функцией Лапласа, для нее составлены таблицы. Существует много разновидностей такой функции, например:

, .

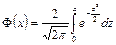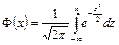Мы будем использовать функцию

.

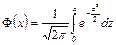(6.22)

Для такой функции табличные значения приведены в Приложении 2.

Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле

.

(6.23)

Рассмотрим свойства случайной величины, распределенной по нормальному закону.

1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал [α, β] равна

,

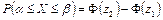(6.24)

где , .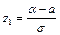

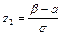2. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания a не превысит величину δ > 0 (по абсолютной величине), равна

,

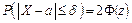(6.25)

где .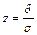

Вычислим по этой формуле вероятности 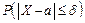при различных значениях δ (используя таблицу значений функции Лапласа):

при δ = σ 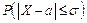= 2Ф(1) = 0,6827;

при δ = 2σ 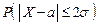= 2Ф(2) = 0,9545;

при δ = 3σ 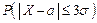= 2Ф(3) = 0,9973.

Отсюда вытекает так называемое «правило трех сигм»:

Если случайная величина Х имеет нормальный закон распределения с параметрами a и σ, то практически достоверно, что ее значения заключены в интервале (a – 3σ; a + 3σ).

Пример 6.3. Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина Х с параметрами а = 173 и σ²= 36, найти:

1. Выражение плотности вероятности и функции распределения случайной величины Х;

2. Долю костюмов 4-го роста (176 – 183 см) и долю костюмов 3-го роста (170 – 176 см), которые нужно предусмотреть в общем объеме производства для данной возрастной группы;

3. Сформулировать «правило трех сигм» для случайной величины Х.

Решение.

1. Находим плотность вероятности

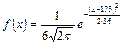
и функцию распределения случайной величины Х

= .

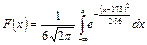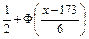2. Долю костюмов 4-го роста (176 – 182 см) находим как вероятность

Р(176 ≤ Х ≤ 182) = = Ф(1,5) – Ф(0,5).

По таблице значений функции Лапласа (Приложение 2) находим:

Ф(1,5) = 0,4332, Ф(0,5) = 0,1915.

Окончательно получаем

Р(176 ≤ Х ≤ 182) = 0,4332 – 0,1915 = 0,2417.

Долю костюмов 3-го роста (170 – 176 см) можно найти аналогично. Однако проще это сделать, если учесть, что данный интервал симметричен относительно математического ожидания а = 173, т.е. неравенство 170 ≤ Х ≤ 176 равносильно неравенству │Х – 173│≤ 3. Тогда

Р(170 ≤Х ≤176) = Р(│Х – 173│≤ 3) = 2Ф(3/6) = 2Ф(0,5) = 2·0,1915 = 0,3830.

3. Сформулируем «правило трех сигм» для случайной величины Х:

Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от а – 3σ = 173 – 3·6 = 155 до а + 3σ = 173 + 3·6 = 191, т.е. 155 ≤ Х ≤ 191. ◄

7. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Как уже говорилось при изучении случайных величин, невозможно заранее предсказать, какое значение примет случайная величина в результате единичного испытания – это зависит от многих причин, учесть которые невозможно.

Однако при многократном повторении испытаний характер поведения суммы случайных величин почти утрачивает случайный характер и становится закономерным. Наличие закономерностей связано именно с массовостью явлений, порождающих в своей совокупности случайную величину, подчиненную вполне определенному закону. Суть устойчивости массовых явлений сводится к следующему: конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений; случайные отклонения от среднего, неизбежные в каждом отдельном явлении, в массе взаимно погашаются, нивелируются, выравниваются.

Именно эта устойчивость средних и представляет собой физическое содержание «закона больших чисел», понимаемого в широком смысле слова: при очень большом числе случайных явлений их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.

В узком смысле слова под «законом больших чисел» в теории вероятностей понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.

Закон больших чисел играет важную роль в практических применениях теории вероятностей. Свойство случайных величин при определенных условиях вести себя практически как не случайные позволяет уверенно оперировать этими величинами, предсказывать результаты массовых случайных явлений почти с полной определенностью.

Возможности таких предсказаний в области массовых случайных явлений еще больше расширяются наличием другой группы предельных теорем, касающихся уже не предельных значений случайных величин, а предельных законов распределения. Речь идет о группе теорем, известных под названием «центральной предельной теоремы». Различные формы центральной предельной теоремы различаются между собой теми условиями, для которых устанавливается это предельное свойство суммы случайных величин.

Различные формы закона больших чисел с различными формами центральной предельной теоремы образуют совокупность так называемых предельных теорем теории вероятностей. Предельные теоремы дают возможность не только осуществлять научные прогнозы в области случайных явлений, но и оценивать точность этих прогнозов.