Закон больших чисел

7.1.1. Неравенство Чебышёва

Для любой случайной величины Х, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышёва:

,

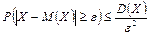(7.1)

т.е. вероятность того, что отклонение случайной величины Х от своего математического ожидания (по абсолютной величине) окажется равно или больше положительного числа ε, не превышает величины D(X) / ε².

В этой форме неравенство устанавливает верхнюю границу вероятности рассматриваемого события.

Учитывая, что события |Х – М(Х)| ≥ ε и |Х – М(Х)| < ε противоположны, неравенство Чебышёва можно записать и в другой форме:

.

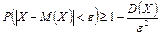(7.2)

В этой форме оно устанавливает нижнюю границу вероятности рассматриваемого события.

Пример 7.1.Оценить вероятность того, что отклонение любой случайной величины от ее математического ожидания по абсолютной величине будет не более трех средних квадратических отклонений (правило трех сигм).

Решение. Учитывая, что D(X) = σ², получаем:

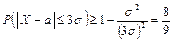= 0,889,

т.е. не менее, чем 0,899. Напомним, что для нормального закона правило трех сигм выполняется с вероятностью Р = 0,9973. Можно показать, что для равномерного закона распределения Р = 1, для показательного – Р = 0,9827 и т.д. Таким образом, правило трех сигм с достаточно большой вероятностью его выполнения, применимо для большинства случайных величин, встречающихся на практике. ◄

7.1.2. Теорема Чебышёва

Теорема. Если дисперсия n независимых случайных величин Х₁, Х₂, …, Х_n ограничена одной и той же постоянной С, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий а₁, а₂, …, а_n, т.е.

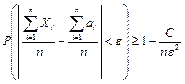
(7.3)

или

.

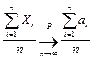(7.4)

Поясним смысл формулировки «сходимость по вероятности». Понятие предела переменной величины Х ( 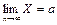) означает, что, начиная с некоторого момента ее изменения для любого (даже сколь угодно малого) числа ε > 0, будет верно неравенство │Х – а│< ε. В круглых скобках выражения (7.3) содержится аналогичное выражение

,

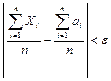где 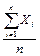– случайная величина, а 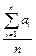– постоянное число.

Однако из (7.3) не следует, что это неравенство будет выполняться всегда, начиная с некоторого момента изменения 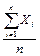. Так как 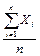– случайная величина, то возможно, что в отдельных случаях неравенство выполняться не будет. Однако с увеличением числа n вероятность неравенства 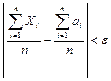стремится к единице, т.е. это неравенство будет выполняться в подавляющем числе случаев. Другими словами, при достаточно больших n выполнение рассматриваемого неравенства является событием практически достоверным, а неравенство противоположного смысла – практически невозможным.

Подчеркнем смысл теоремы Чебышёва. При большом числе случайных величин практически достоверно, что их средняя 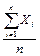– величина случайная, как угодно мало отличается от неслучайной величины 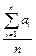, т.е. практически перестает быть случайной.

Следствие. Если независимые случайные величины Х₁, Х₂, …, Х_n имеют одинаковые математические ожидания, а их дисперсии ограничены одной и той же постоянной, то формулы теоремы Чебышёва принимают вид:

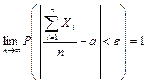
(7.5)

или

.

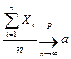(7.6)

Теорема Чебышёва и ее следствие имеют большое практическое значение. Например, страховой компании необходимо установить размер страхового взноса, который должен уплачивать страхователь. При этом страховая компания обязуется выплатить при наступлении страхового случая определенную страховую сумму. Рассматривая частоту страховых случаев как величину случайную и обладая статистикой таких случаев, можно определить среднее число страховых случаев, которое на основании теоремы Чебышёва с большой степенью уверенности можно считать величиной почти не случайной. Тогда на основании этих данных и предполагаемой страховой суммы определяется размер страхового взноса.

Другой пример.

Пример 7.2.Сколько надо провести измерений случайной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины менее, чем на 1 (по абсолютной величине), если среднее квадратическое отклонение каждого из измерений не превосходит 5?

Решение. Используя теорему Чебышёва, найдем n, при котором

.

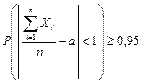Данное неравенство будет выполняться, если

,

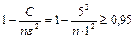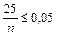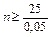откуда и = 500, т.е. потребуется не менее 500 измерений. ◄

Отметим важные частные случаи теоремы Чебышёва: теоремы Бернулли и Пуассона.

Теорема Бернулли

Теорема. Частость события в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р, при неограниченном увеличении числа испытаний сходится по вероятности к вероятности этого события в отдельном испытании:

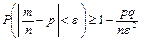
(7.7)

или

.

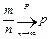(7.8)

Теорема Бернулли дает теоретическое обоснование замены неизвестной вероятности события его частостью, или статистической вероятностью, полученной в n повторных независимых испытаниях.

Непосредственным обобщением теоремы Бернулли является теорема Пуассона, когда вероятности события в каждом испытании различны.

Теорема Пуассона

Теорема. Частость события в n повторных испытаниях, в каждом из которых оно может произойти соответственно с вероятностями р₁, р₂, …р_n при неограниченном увеличении числа испытаний сходится по вероятности к средней арифметической вероятностей события в отдельном испытании:

.

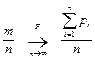(7.9)

Закон больших чисел может быть распространен и на зависимые случайные величины. Обобщение закона больших чисел на случай зависимых случайных величин принадлежит А. А. Маркову.

Теорема Маркова

Теорема. Если имеются зависимые случайные величины Х₁, Х₂, …, Х_n и если при n→ ∞ выполняется условие

,

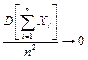(7.10)

то среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий

.

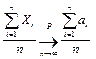(7.11)