Показательный (экспоненциальный) закон распределения
Определение. Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности f(x) имеет вид:
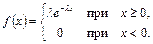
| (6.13) |
Кривая распределения f(x) и график функции распределения F(x) случайной величины Х приведены соответственно на рис. 7.3 и рис. 7.4.
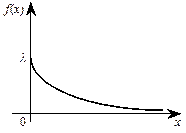
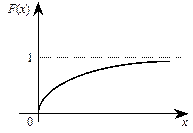
Рис. 7.3 Рис. 7.4
Теорема. Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону, есть
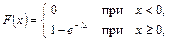
| (6.14) |
ее математическое ожидание
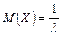 , ,
| (6.15) |
а дисперсия
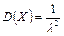 . .
| (6.16) |
Отсюда следует, что для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т.е.
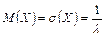 .
.
Вероятность попадания в интервал [a; b] непрерывной случайной величины Х, распределенной по показательному закону, находится как
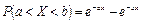 . .
| (6.17) |
Пример 6.1. Установлено, что время ремонта железнодорожных вагонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт вагона потребуется менее 7 дней, если среднее время ремонта вагонов составляет 10 дней.
Решение. По условию математическое ожидание М(Х) = 1/λ = 10, откуда параметр λ = 0,1. По формуле (6.17) находим вероятность попадания случайной величины Х в интервал [0, 7]:
Р(0 < Х < 7) = е-0,1·0 – е-0,1·7 = 1 – е-0,7 ≈ 0,503. ◄
Показательный закон распределения играет большую роль в теории массового обслуживания. Так например, интервал времени между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром λ – интенсивностью потока.
Кроме того, показательное распределение широко применяется в теории надежности, одним из основных понятий которой является функция надежности.
Функция надежности
Будем называть элементом некоторое устройство. Пусть элемент начинает работать в момент времени τ0 = 0, а по истечении времени τ происходит отказ.
Обозначим через Т непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно (т.е. до наступления отказа) время, меньшее чем τ, то, следовательно, за время длительностью τ наступил отказ.
Таким образом, интегральная функция
F(τ) = P(T < τ)
определяет вероятность отказа за время длительностью τ. Следовательно, вероятность безотказной работы за это же время, длительностью τ, т.е. вероятность противоположного события Т > τ, равна
R(τ) = P(T > τ) = 1 – F(τ).
Функцией надежности R(τ), называют функцию, определяющую вероятность безотказной работы элемента за время длительностью τ:
| R(τ) = P(T > τ) = e–λτ, | (6.18) |
где λ – интенсивность отказов.
Широкое использование показательного закона распределения обусловлено тем, что только он обладает следующим важным свойством:
Если промежуток времени Т, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения оставшейся части Т1 = Т – τ промежутка, т.е. закон распределения Т1 остается таким же, как и всего промежутка Т.
Пример 6.2. Время безотказной работы устройства распределено по показательному закону f(t) = 0,02e-0,02t при t ≥ 0 (t – время в часах). Какова вероятность того, что устройство проработает безотказно 50 часов?
Решение. По условию постоянная интенсивность отказов λ = 0,02. Используя формулу (6.18), получаем:
R(50) = e-0,02·50 = e-1 ≈ 0,368. ◄
Дата добавления: 2015-11-10; просмотров: 4141;
