Мода и медиана. Квантили

Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.

Определение. Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность p_i или плотность вероятности f(x) достигает максимума).

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.

Определение. Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого

Р(Х < Ме(Х)) = Р(Х > Ме(Х)) =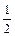

(5.20)

т. е. вероятность того, что случайная величина Х примет значение, меньшее медианы или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая х = Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точке х = Ме(Х) функция распределения равна 1/2.

Пример 5.3. Найти моду, медиану случайной величины Х с плотностью вероятности f(x) = 3х² при х 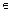[0; 1].

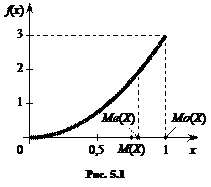Решение. Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1.

Медиану Ме(Х) = найдем из условия (5.20):

,

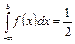или

,

откуда . ◄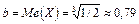

Наряду с модой и медианой для описания случайной величины используется понятие квантиля.

Определение. Квантилем уровня q (или q-квантилем) называется такое значение х_q случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.

Пример 5.4. По данным примера 5.3 найти квантиль х_0,3.