Математическое ожидание случайной величины
Определение. Математическим ожиданием, или средним значением, M(X) дискретной случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
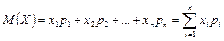 . .
| (5.1) |
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся х, а вероятность pi – элементом вероятности f(x)dx. Получаем формулу для математического ожидания непрерывной случайной величины (если интеграл абсолютно сходится):
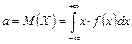 . .
| (5.2) |
Рассмотрим свойства математического ожидания.
1. Математическое ожидание постоянной величины равно самой постоянной:
| М(С) = С. | (5.3) |
2. Постоянный множитель можно выносить за знак математического ожидания, т.е.
| M(СX) = С·M(X). | (5.4) |
3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е.
М(X 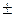 Y) = M(X) Y) = M(X) 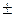 M(Y). M(Y).
| (5.5) |
4. Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е.
| M(XY) = M(X)·M(Y). | (5.6) |
5. Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
М(X 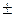 С) = M(X) С) = M(X) 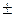 С. С.
| (5.7) |
6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
| M[X – M(X)] = 0. | (5.8) |
Пример 5.1. Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение. Используя свойства 1, 2, 3 математического ожидания, находим
M(Z) = 8M(X) – 5M(Y) + M(7) = 8·3 – 5·2 + 7 = 21. ◄
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину.
Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дата добавления: 2015-11-10; просмотров: 1852;
