Закон распределения случайной величины
Наиболее полным, исчерпывающим описанием случайной величины является ее закон распределения.
Определение. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Про случайную величину говорят, что она «распределена» по данному закону распределения или «подчинена» этому закону.
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически или графически.
Простейшей формой задания закона распределения дискретной случайной величины X является таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины и соответствующие им вероятности, т.е.
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
Такая таблица называется рядом распределения дискретной случайной величины.
Отметим, что события X = x1, X = x2, …, X = xn, состоящие в том, что в результате испытания случайная величина Х примет соответственно значения x1, x2, …, xn, являются несовместными и единственно возможными, т.е. образуют полную группу. Следовательно, сумма их вероятностей равна единице, т.е.
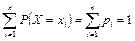 . .
| (4.1) |
Ряд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, а оси ординат – соответствующие им вероятности. Соединение полученных точек образует ломаную линию, которую называют многоугольником или полигоном распределения вероятностей.
Пример 4.1. Два стрелка делают по одному выстрелу в мишень. Составить закон распределения случайной величины Х – общего числа попаданий в мишень, если вероятность поражения мишени в одном выстреле для первого стрелка равна 0,8, а для второго – 0,6.
Решение. Очевидно, что возможные значения Х – 0, 1, 2. Пусть А1 – событие состоящее в том, что первый стрелок попадет в мишень, А2 – второй стрелок попадет в мишень. Тогда
Р(Х = 0) = Р( 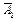
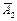 ) = Р(
) = Р( 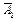 )·Р(
)·Р( 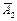 ) = (1 – 0,8)(1 – 0,6) = 0,2·0,4 = 0,08;
) = (1 – 0,8)(1 – 0,6) = 0,2·0,4 = 0,08;
Р(Х = 1) = Р(А1 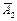 +
+ 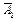 А2) = Р(А1)·Р(
А2) = Р(А1)·Р( 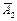 ) + Р(
) + Р( 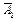 )·Р(А2) = 0,8·0,4 + 0,2·0,6 = 0,44;
)·Р(А2) = 0,8·0,4 + 0,2·0,6 = 0,44;
Р(Х = 2) = Р(А1А2) = Р(А1)·Р(А2) = 0,8·0,6 = 0,48.
Записываем ряд распределения случайной величины Х.
| xi | |||
| pi | 0,08 | 0,44 | 0,48 |
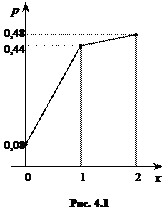 На рис. 4.1 полученный ряд распределения представлен графически в виде многоугольника (полигона) распределения вероятностей случайной величины Х. ◄
На рис. 4.1 полученный ряд распределения представлен графически в виде многоугольника (полигона) распределения вероятностей случайной величины Х. ◄
Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина. Так если случайная величина Х может принимать значения xi (i = 1, 2, …, n), а случайная величина Y – значения yj(j = 1, 2, …, m), то независимость случайных величин X и Y означает независимость событий X = xi и Y = yj при любых i = 1, 2, …, n и j = 1, 2, …, m. В противном случае случайные величины называются зависимыми.
Дата добавления: 2015-11-10; просмотров: 1305;
