Локальная теорема Муавра-Лапласа

Теорема. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна

,

(3.3)

где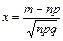

.

(3.4)

Эта приближенная формула тем точнее, чем больше n и чем ближе к 0,5 значения p и q. Вычисление по этой формуле дает незначительную погрешность при выполнении условия npq ≥ 20, хотя допустимым можно считать выполнение условия npq > 10.

Для упрощения расчетов, связанных с применением локальной формулы Муавра-Лапласа, составлена таблица значений функции φ(x) (см. Приложение 1). Пользуясь этой таблицей, необходимо иметь в виду следующие свойства функции φ(x):

1. Функция φ(x) является четной, т.е. φ(–x) = φ(x).

2. Функция φ(x) – монотонно убывающая при положительных значениях x, причем при x → ∞ φ(x) → 0 (практически можно считать, что уже при x ≥ 5 φ(x)≈0).

Пример 3.3. По результатам многолетних наблюдений известно, что экзамен по теории вероятностей с первого раза успешно сдают в среднем 80% студентов. Найти вероятность того, что из 400 студентов 2-го курса 300 успешно сдадут экзамен с первого раза.

Решение. По условию n = 400, m = 300, p = 0,8, q = 0,2. Так как npq=400·0,8·0,2 = 64 > 20, то условие применимости локальной формулы Муавра-Лапласа (npq ≥ 20) выполняется.

Вначале определяем 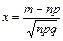= = – 2,5.

По таблице значений функции φ(x) находим φ(– 2,5) = 0,0175.

Находим вероятность того, что ровно 300 студентов из 400 успешно сдадут экзамен с первого раза:

≈ 0,0022.

Относительно малое значение вероятности не должно вызывать сомнений, так как кроме события «ровно 300 студентов успешно сдадут экзамен с первого раза» возможно еще 400 событий: «0 из 400», «1 из 400» и т.д. Каждое из этих событий обладает своей вероятностью, а все вместе они образуют полную группу событий и, следовательно, сумма их вероятностей равна единице. ◄

Пусть в условиях этого примера необходимо найти вероятность того, что от 300 до 360 студентов (включительно) успешно сдадут экзамен с первого раза. В этом случае по теореме сложения вероятность искомого события

P₄₀₀(300 ≤ m ≤ 360) = P₄₀₀(300) + P₄₀₀(301) + … + P₄₀₀(360).

В принципе каждое слагаемое можно вычислить по локальной формуле Муавра-Лапласа, но большое число слагаемых делает расчет весьма громоздким. В таких случаях используется интегральная теорема Лапласа.