Вероятность появления хотя бы одного события. Теорема. Вероятность появления хотя бы одного из событий А1, А2, ,Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей

Теорема. Вероятность появления хотя бы одного из событий А₁, А₂,…,А_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий :

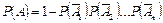
(2.7)

Пример 2.5. Три стрелка делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,7, второго – 0,8 и третьего – 0,9. Найти вероятность того, что хотя бы один стрелок попадет в мишень.

Решение. Рассмотрим следующие события: А – хотя бы один стрелок попадет в мишень А₁ – первый стрелок попадет в мишень, А₂ – второй стрелок, А₃ – третий стрелок. Вероятность попадания в мишень каждым из стрелков не зависит от результатов стрельбы других стрелков, поэтому события А₁, А₂ и А₃ независимы в совокупности.

Вероятности событий, противоположных событиям А₁, А₂ и А₃ (т.е. вероятности промахов), соответственно равны:

= 1 – 0,7 = 0,3;

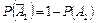= 1 – 0,8 = 0,2;

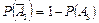= 1 – 0,9 = 0,1.

Искомая вероятность

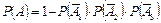= 1 – 0,3·0,2·0,1 = 0,994. ◄

Частный случай. Если события А₁, А₂,…,А_n имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий

где q = 1 – p.