Зависимые и независимые события
Определение. Два события называют независимыми, если вероятность появления одного из них не зависит от того, произойдет другое событие или нет.
Например, опыт состоит в бросании двух монет. Пусть А и В – события, состоящие в том, что герб появится соответственно на первой и второй монете. В данном случае вероятность события А не зависит от того, произошло событие В или нет. Следовательно, событие А независимо от события В.
Определение. Несколько событий называют попарно независимыми, если каждые два из них независимы.
Например, опыт состоит в бросании трех монет. Пусть А, В, С – события, состоящие в том, что герб появится соответственно на первой, второй и третьей монете. В данном случае каждые два из рассматриваемых событий (т.е. А и В, А и С, В и С) – независимы. Следовательно, события А, В и С – попарно независимые. ◄
Определение. Два события называют зависимыми, если вероятность появления одного из них меняется в зависимости от того, произойдет другое событие или нет.
Например, в урне 3 белых и 2 черных шара. Наудачу берут один шар, не возвращая его в урну. Если появился белый шар (событие А), то вероятность появления белого шара во втором испытании (событие В) Р(В) = 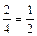 . Если же в первом испытании появился черный шар (т.е. событие А не произошло), то вероятность Р(В) =
. Если же в первом испытании появился черный шар (т.е. событие А не произошло), то вероятность Р(В) =  . Т.е. вероятность события В зависит от того, произошло событие А или нет. Следовательно, события А и В – зависимые.
. Т.е. вероятность события В зависит от того, произошло событие А или нет. Следовательно, события А и В – зависимые.
Отметим, что зависимость и независимость событий всегда взаимны, т.е. если событие В не зависит от события А, то и событие А не зависит от события В.
Дата добавления: 2015-11-10; просмотров: 1121;
